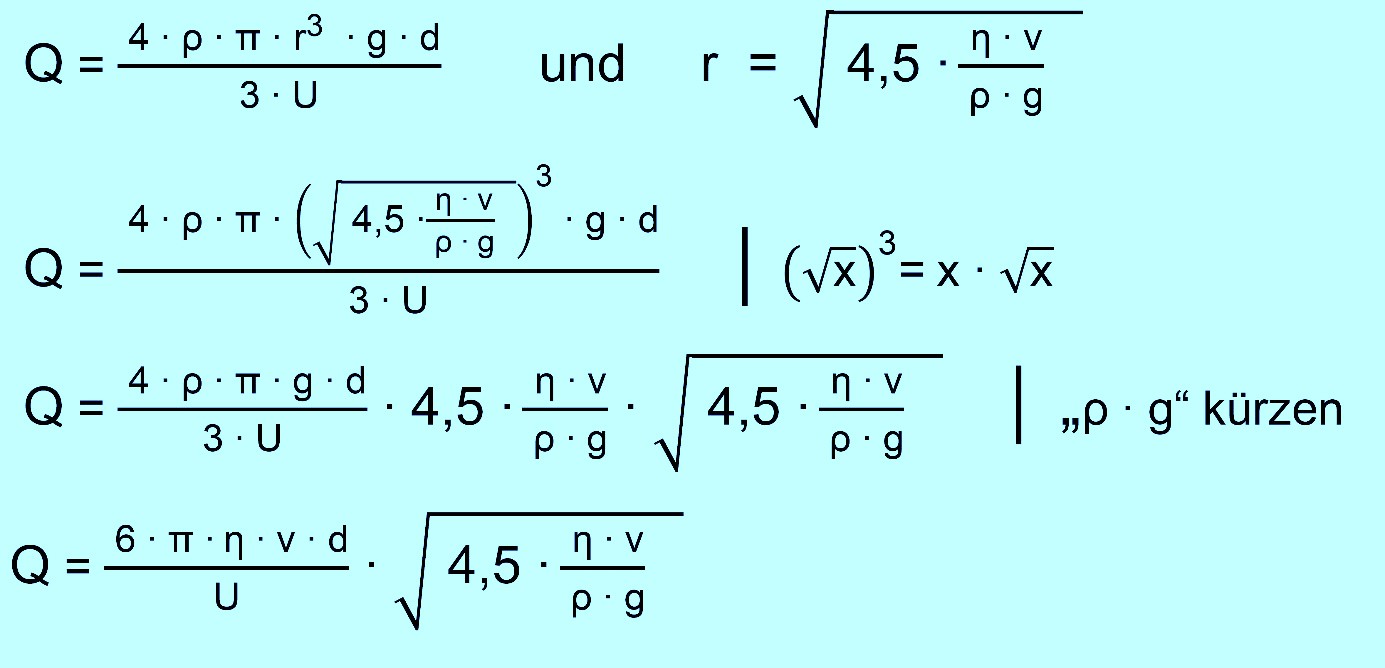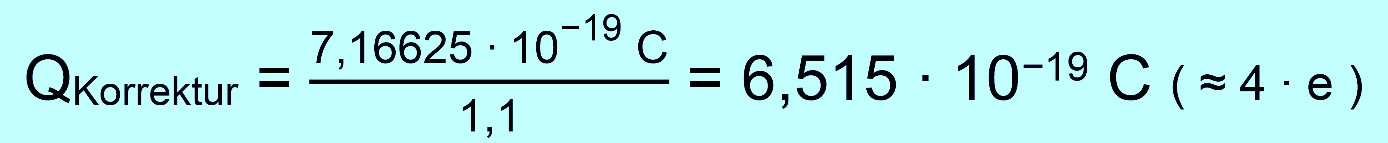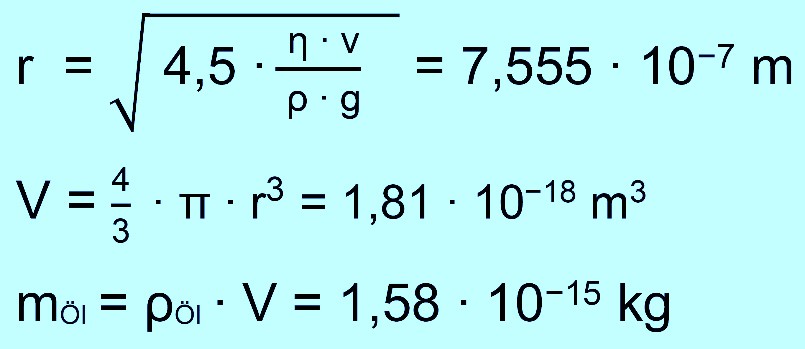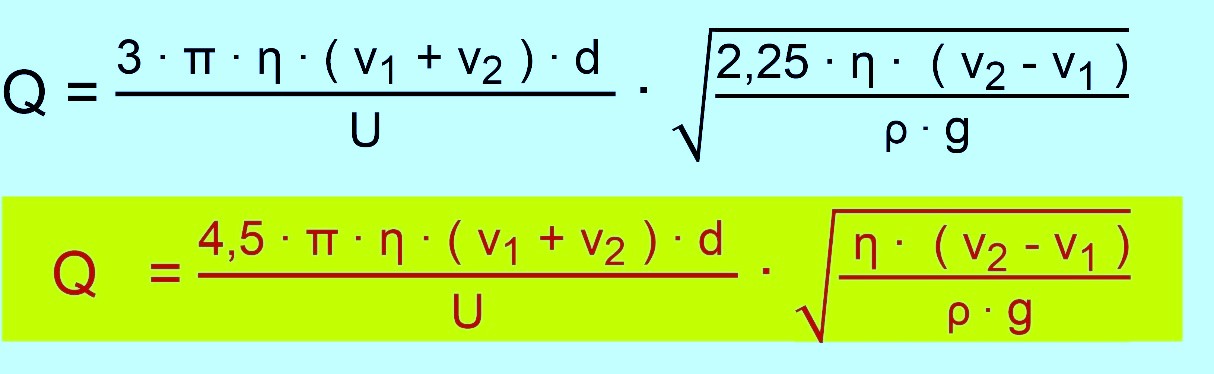|
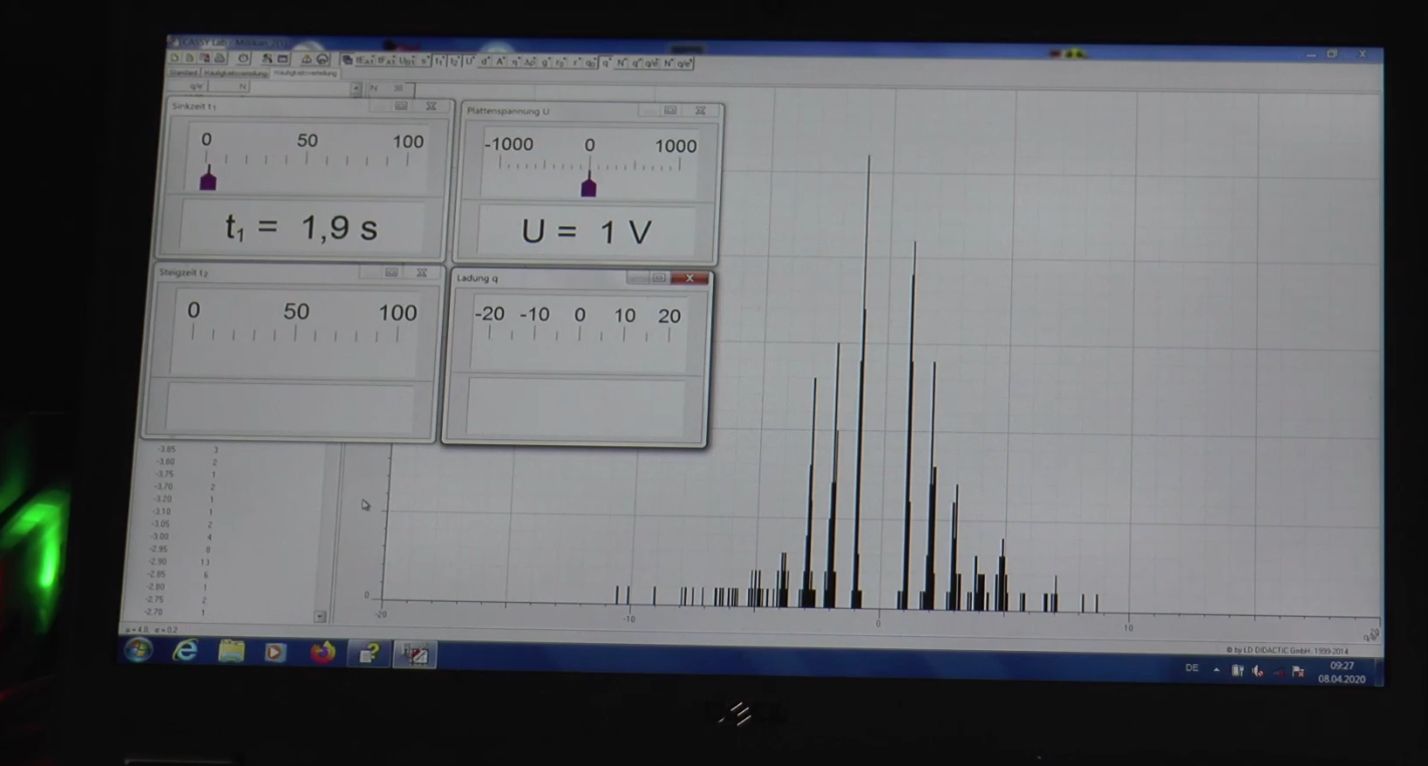
Aufbau Ziel des Versuches am Anfang des 20. Jhd. war es die Größe der Ladung von Öltröpfen zu bestimmen. Im Folgenden wird der häufig im Unterricht übliche Aufbau gezeigt. Alle Abbildungen entstammen aus dem Video von Benno Köhler, dass anschließend betrachtet werden kann. Die Abbildungen sind von mir mit Benennungen versehen worden. 1. Abbildung: Gesamtaufbau
Beschreibung: Der wesentliche Teil des Aufbaus ist der horizontal liegende Platten- kondensator. Dieser kann über das Netzgerät mit variablen Span- nungen versorgt werden. Durch das Mikroskop kann man mit einer gewissen Vergrößerung in den Plattenkondensator hineinschauen und die Öltröpfen beobachten, die über den Zerstäuber hineinge- blasen werden. Durch den Sprühvorgang werden durch die Reibung am Sprühkopf die Öltröpfchen aufgeladen. Da man die Öltröpfchen nicht direkt erkennen kann, werden diese beleuchtet, so dass das ge- streute Licht das Öltröpfchen sichtbar macht. Diese Lichtpunkte kön- nen z.T. sehr klein sein, wenn die Öltröpfchen sehr klein sind, z.Bsp. wenn ein anderer Zerstäuber (z.B. üblicher Parfüm-Zerstäuber) be- nutzt wird. 2. Abbildung: Betriebsgerät
Beschreibung: Das Betriebsgerät stellt die Spannung für die Beleuchtung und die Spannungen für den Kondensator zur Verfügung. Die Spannung kann reguliert werden, wobei man die angelegte Spannung an einem Mess- gerät ablesen kann. Da die Geschwindigkeit der Öltröpfchen gemes- sen wird, können zwei Stoppuhren angeschlossen werden. Es ist aber auch möglich ganz normale Handstoppuhren zu benutzen. 3. Abbildung: Skala im Mikroskop
Beschreibung: Im Mikroskop befindet sich eine Skala, mit der man die Geschwindig- keit der Tröpfchen messen kann. Man kann die zurückgelegte Strecke an der Skala ablesen. Ohne Spannung fallen alle Öltröpfchen aufgrund der Gewichtskraft! Hinweis:
1.) In der
Abbildung Nr.3 ist die Fall- bzw. Steigbewegung in unterschiedliche
Richtungen eingetragen. Dies liegt daran, dass beim alten Leybold-Gerät 559 41/42 das Bild auf dem Kopf steht, so dass die Fallbewegung nach oben zeigt. Bei dem neuen Gerät 559 412 ist dies vor das enden Öltröpfchen tatsächlich bewegen. Man bekommt immer Klarheit, indem man keine
Spannung
(+ Reibung)
bewegen. 2.) Im
alten Leybold-Gerät 559 41/42 berechnet sich die
Strecke über s = x/1,875 ∙ 10−4 m. Dies
bedeutet, dass ein Skalenteil 0,1 mm entspricht, wobei das Mikroskop mit
1,875 ver- größert
(x = Anzahl der Skalenteile). Im neuen Gerät muss 1,875 durch 2 ersetzt
werden. (zu den
neuen Leybold-Geräten: s. Linkliste) Im Folgenden sieht man einen Ausschnitt aus dem Video von Benno Köhler, in dem er den Aufbau erklärt. Quelle: Physik LK 7 -
Millikan Versuch - YouTube (Ausschnitt) Bestimmung der
Ladung Es sind zunächst einmal zwei Versuchsdurchführungen üblich: 1.) Schwebemethode mit anschließendem Abschalten der Spannung (Schwebe-Sinkmethode) 2 a.) Steig-Sink-Methode mit E-feld zum Steigen und Sinken ohne Feld (Leybold neu) 2 b.) Steig-Sink-Methode mit jeweils umgekehrter Spannung (Benno) Kräftebetrachtung Es
können insgesamt vier Kräfte auf ein Öltröpfchen einwirken. Dies
sind: 1.) die
elektrische Kraft, wenn eine Spannung anliegt 2.) die
Gewichtskraft, weil das Tröpfchen eine Masse hat 3.) die
Auftriebskraft, weil sich das Tröpfchen in der Luft befindet 4.) die
Reibungskraft, weil sich das Tröpfchen durch die Luft bewegt Uns
vertraut sind die ersten beiden Kräfte. zu 1.) elektrische Feldkraft Die elektrische Feldkraft wirkt
auf alle geladenen Teilchen, wenn sie sich in
einem elektrischen Feld befinden. Dies ist hier der Fall, wenn eine
Spannung am Kondensator anliegt. Dann befindet sich zwischen den
Kondensatorplatten ein homogenes elektrisches Feld. Für die
Kraft gilt: FE = Q ∙ U/d Die Bewegungsrichtung im elektrischen Feld hängt von der Art der Ladung ab. Positive Teilchen bewegen sich in Feldlinienrichtung, negative Teilchen in die entgegengesetzte Richtung. zu 2.) Gewichtskraft Die Gewichtskraft wirkt immer auf eine Masse. Es gilt hierfür: FG = mÖl ∙ g zu 3.) Auftriebskraft Diese Kraft ist vielen noch aus der Mittelstufe bekannt. Es gilt das „Archimedische Prinzip“. Die Auftriebskraft ist so groß wie die Gewichtskraft der verdrängten Luft. Es gilt somit: FA = mLuft ∙ g = ρLuft ∙ VLuft
∙ g zu 4.) Reibungskraft Die Betrachtungen hierzu gehen deutlich über die Inhalte der Physik der Oberstufe hinaus, da strömungsmechanische Inhalte nicht vorge- sehen sind. Wir geben daher hier die Formeln einfach an. Für kugelförmige Körper, die sich durch
ein homogenes Gas be- wegen,
gilt das Gesetz von Stokes. Es muss eine laminare Strömung, d.h.
ohne Turbulenz, vorliegen. Dann
gilt für die Reibungskraft: FR = 6 ∙ π ∙
η ∙ v ∙ r Legende: d = Abstand der Platten = 6 mm = 0,006 m g = Fallbeschleunigung = 9,81 m/s2 m = Masse V = Volumen ρLuft = Dichte der Luft = 1,29 kg/m3 Hinweis:
dieser Wert wird üblicherweise genannt, dürfte aber zu hoch sein, da T = 0°C
angenommen wird;
spielt aber in der Rechnung keine große Rolle (s.dort) ρÖl = Dichte des Öls = 875,3 kg/m3 v =
Geschwindigkeit r =
Radius η =
Viskosität = 1,81 ∙ 10−5 Ns/m2 Schwebe-Sink-Methode Vorgehen: Zunächst
wird die Spannung so eingestellt. dass das Tröpfchen schwebt.
Die Schwebespannung Us wird gemessen.
Danach wird die
Spannung abgeschaltet. Das Tröpfchen fällt unter der Gewichts- kraft.
Man misst die Geschwindigkeit v des Tropfens. Theorie:
Schweben Im
Schwebezustand wird die nach unten zeigende Gewichtskraft durch
die nach oben zeigende elektrische Feldkraft und Auftriebs- kraft ausgeglichen. Eine Reibungskraft tritt nicht auf, weil sich das Tröpfchen
nicht bewegt. Die
Abbildung zeigt noch einmal die Verhältnisse.
Es
ergeben sich dann folgende Gleichungen zur Berechnung von Q.
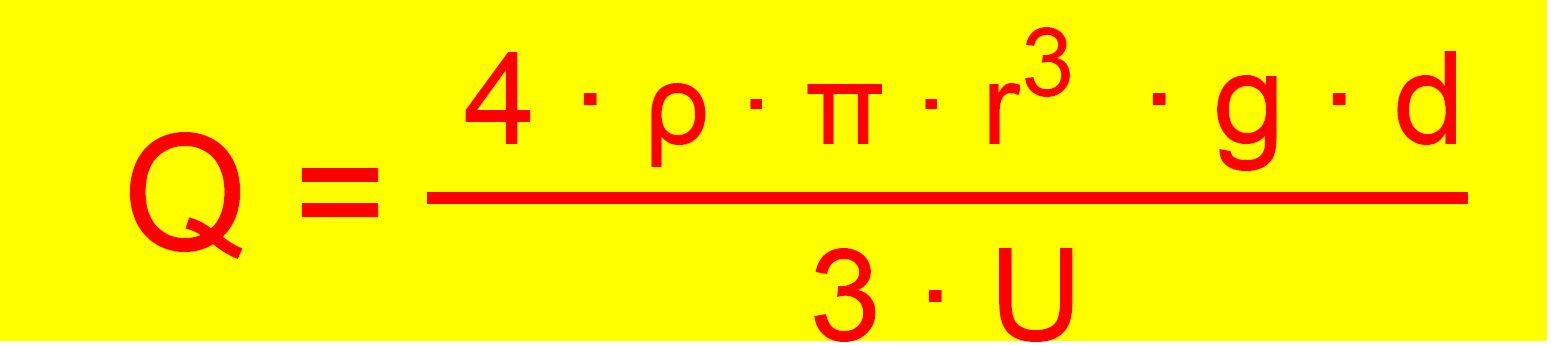
Für Q
gilt also letztendlich:
Es sind
fast alle Größen, wie „ρ, d und U“ bekannt. Nur der Radius r des
Öltröpfchens kann nicht angegeben werden. Das Öltröpfchen ist viel
zu klein und macht sich ja nur durch die Lichtstreuung bemerk- bar. Der
Radius wird jetzt über das Sinken gewonnen. Theorie:
Sinken Auch hier
zunächst eine Abbildung zu den Verhältnissen.
Da keine
Spannung anliegt, gibt es keine elektrische Feldkraft. Das Tröpfchen sinkt unter der Einwirkung der Gewichtskraft und wird be- schleunigt (Grundgleichung der Mechanik). Dabei steigt die Geschwin- digkeit v an, so dass auch die Reibungskraft steigt. Nach kurzer Zeit sind Auftriebskraft und Reibungskraft so groß wie die Gewichtskraft und halten sich die Waage. Die resultierende Kraft hat 0 N. Die Be- schleunigung wird 0 m/s2, so dass sich eine konstante Geschwindig- keit v einstellt. Es
ergeben sich folgende Gleichungen zur Berechnung von r.
Für r
gilt also:
Wir
führen jetzt die beiden Gleichungen zusammen, d.h. wir setzen die
Gleichung für r in die erste Gleichung für Q ein. Es
ergibt sich:
Einsetzen
der Werte von oben ergibt am Schluss:
U = Spannung zum Schweben v = Geschwindigkeit beim Fallen
ohne Feld Eigene Messergebnisse für
Schwebe-Sink-Methode Es ist leider im Unterricht üblich geworden, die realen Messungen durch Simulationen (vor allem bei Leifi) zu ersetzen. Wobei dies meiner Meinung nach völlig unnötig ist, zumal die Simulation die Rea- lität immer nur nachbilden kann und nicht ersetzen sollte. Beim Millikanversuch ist es mir schon mehrfach gelungen mit den Leybold- Geräten sehr zufriedenstellende Ergebnisse mit der Schwebe-Sink- Methode zu erreichen. Hier einige Beispiele: 1.
Messung (LK 14-15) U = 130 V , t = 8,87 s für 10 Skalenteile
Wenn man
das eigentliche Ergebnis des Millikanversuches (s.
unten) schon
einmal vorwegnimmt, würde man sagen, dass dieses Ergebnis nicht
besonders gut ist, weil es gerade ca. 4,5 e entspricht. Dies
hängt aber damit zusammen, dass die Voraussetzungen für das Reibungsgesetz
von Stokes nicht vollständig erfüllt sind. Die Öl- tröpfchen
sind so klein, dass keine homogene Luftmasse mehr vor- liegt
durch die sich das Tröpfchen bewegt. Das Tröpfchen trifft seltener auf Luftmoleküle,
als es bei Stokes sein sollte. Dies
wird durch einen Korrekturfaktor von Cunningham behoben. Wer dies
genauer ergründen will, sollte in der Linkliste fündig werden. Für die
Oberstufenphysik führt dies viel zu weit. Wir
halten nur das Resümee fest. In den Leyboldunterlagen
wird ein Faktor
von 1,1 angenommen. Dies
bedeutet, dass man den berechneten Ladungswert noch durch 1,1
teilen muss, um den exakten Wert für Q zu erhalten. Er
ergibt sich dann:
Wir
haben eine Genauigkeit von 98% erzielt, was für einen Schulver- such
schon beachtlich ist. Im
Folgenden sieht man noch zusätzlich Berechnungen zu den Größen
r, V und m. Man erkennt, dass es sich um extrem kleine Werte
handelt. Hinweis: r liegt in der Größenordnung der mittleren
Weglänge von Luftmolekülen (100 nm), so das Stokes nicht mehr vollständig zutrifft.
weitere
Messergebnisse: 2.) LK
07/08 U = 76 V, t = 22,2s für 20
Skalenteile → s = 10,66 ∙ 10−4 m,
v = 4,8048 ∙ 10−5 m/s, Q =
8,765 ∙ 10−19 C, →
QKorrektur = 7,968 ∙ 10−19 C ( ≈ 5 e, 99,5%) 3.) LK
17/18 U = 136,5 V, t = 14,38 s für 10
Skalenteile → s = 5,33 ∙ 10−4 m, v
= 3,70885 ∙ 10−5 m/s, Q =
3,3095 ∙ 10−19 C, →
QKorrektur = 3,00864 ∙ 10−19 C ( ≈ 2 e, 94%) 4.) LK
99/00 U = 40 V, t= 39,3 s für 20
Skalenteile → s = 10,66 ∙ 10−4 m,
v = 2,71416 ∙ 10−5 m/s, Q =
7,07006∙ 10−19 C, →
QKorrektur = 6,4273 ∙ 10−19 C ( ≈ 4 e, 100,3%) 5.) ???? U = 80 V, t = 21,45 s für
20 Skalenteile → s = 10,66 ∙ 10−4 m,
v = 4,96970 ∙ 10−5 m/s, Q =
8,7586 ∙ 10−19 C, →
QKorrektur = 7,9624 ∙ 10−19 C ( ≈ 5 e, 99,4%) Steigen-Sinken(ohne E)-Methode Vorgehen: Man
stellt eine feste Spannung U ein und beobachtet die Bewegung eines
Öltröpfchens beim Steigen. Die Zeit für eine bestimmte Skalen- anzahl
wird gemessen. Danach entfernt man die Spannung und lässt das
Öltröpfchen ohne elektrisches Feld fallen (s. Schwebe-Sink-Methode) Theorie:
Steigen Hier
zunächst eine Abbildung zu den Verhältnissen.
Wegen des elektrischen Feldes bewegt sich das Öltröpfchen nach oben. Ebenfalls nach oben zeigt die Auftriebskraft. Es stellt sich wieder eine konstante Geschwindigkeit v1
ein, d.h. die Gewichts- kraft und die Reibungskraft haben die gleiche Größe wie die beiden anderen Kräfte. Es ergeben sich folgende Gleichungen (v1 = Steiggeschwindigkeit):
Theorie:
Sinken ohne Feld Diesen
Fall haben wir ja oben (s. Schweben-Sinken) schon behandelt. Es gilt also (v0 = Fallgeschwindigkeit):
Man wählt jetzt r von oben und erhält somit insgesamt:
Einsetzen der Zahlenwerte (s.oben) ergibt dann als Endgleichung.
U = Spannung zum Steigen v0 = Geschwindigkeit
beim Fallen ohne Feld v1
= Geschwindigkeit beim Steigen mit Feld Steigen-Sinken(mit E)-Methode Vorgehen: Man
stellt eine feste Spannung U ein und beobachtet die Bewegung eines
Öltröpfchens beim Steigen. Die Zeit für eine bestimmte Skalen- anzahl
wird gemessen. Danach polt man die Spannung um und lässt das
Öltröpfchen im elektrischen Feld fallen. Theorie:
Steigen Es ergibt sich nichts Neues. Wir haben die Verhältnisse wie oben (Steigen-Sinken(ohne E)-Methode). Also gilt:
Theorie:
Sinken mit Feld Abbildung
hierzu
Gleichungen (v2 = Fallgeschwindigkeit)
Am Schluss ergibt sich also durch Einsetzen von r
Einsetzen der Zahlenwerte (s.oben) ergibt dann als Endgleichung.
U = Spannung zum Steigen und Fallen v2 = Geschwindigkeit
beim Fallen mit Feld v1 = Geschwindigkeit beim Steigen mit Feld Hier einmal ein Video zur Methode 1.) (nicht vollständig) und 2.a.). Quelle: https://www.youtube.com/watch?v=sb30LcAYPYY
(Ausschnitt) Resümee: Von den Formeln her ist auf jeden Fall die erste Methode das ein- fachste Verfahren zur Bestimmung von Q. Es führt auch, wie meine Messungen zeigen, zu ausgezeichneten Ergebnissen. Vielfach wird kritisiert, dass man den Schwebefall schlecht einstellen kann, was ich nicht bestätigen kann. Ergebnisse und
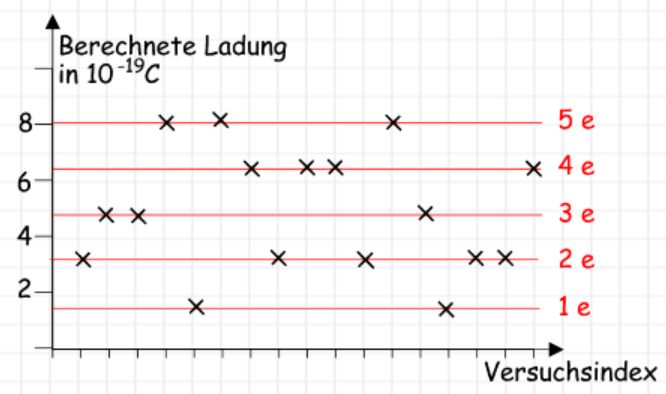
Schlussfolgerungen Millikan stellt fest, dass die Ergebnisse seiner Messungen nicht beliebige Ladungswerte ergeben. Es gibt
keine kontinuierliche Verteilung der
Ladungswerte, sondern es sind nur ganz
bestimmte Ladungswerte
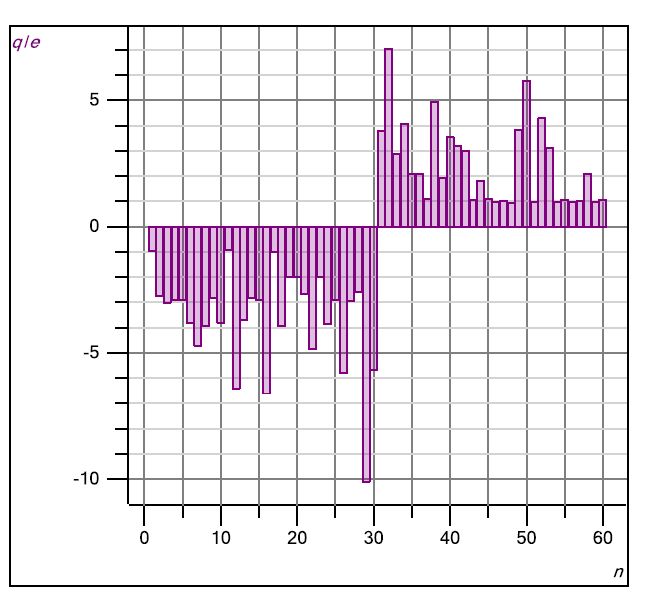
möglich. Diese sind immer Vielfache einer kleinsten Ladung, die als Elementarladung bezeichnet wird. Die Ladung gibt es also nur portionsweise. Man spricht auch von der Quantelung der Ladung. Die Elementarladung wird häufig mit „e“ abgekürzt. Neben meinen Ergebnissen von oben, werden in den folgenden Abbildungen weitere Ergebnisse gezeigt. 1. Fall: Firma Leybold Hier sind die Ergebnisse schon als Vielfache von e angegeben. Es gibt negative und positive Werte.
Quelle: Handblatt
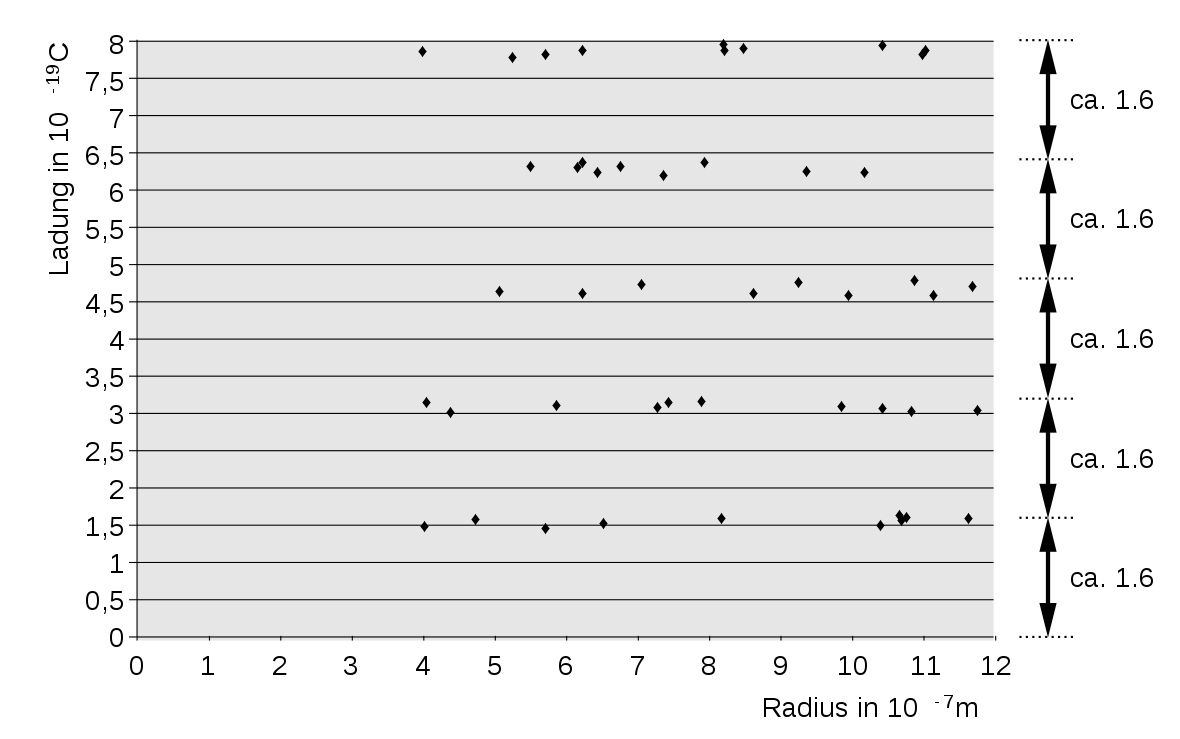
zum Millikan-Versuch 2. Fall: wikipedia Die Ergebnisse sind gegen den Radius aufgetragen.
Quelle: Millikan-Versuch –
Wikipedia 3. Fall. Schematisch wird es auf den roro-seiten so dargestellt.
Quelle: Millikanversuch-Durchführung (roro-seiten.de) Zusammenfassung des Millikan-Versuches
Linkliste:
zum
Abschnitt: -
Versuchsaufbau - verschiedene Versuchsabläufe -
Kräftebetrachtung - Schwebe-Sink-Methode -
Steig-Sink(ohne Feld)-Methode - Steig-Sink(mit
Feld)-Methode - Messergebnisse Beck - Millikan-Messergebnisse-Grafik - Zusammenfassung Millikan-Elementarladung - Kapitel
„Plattenkondensator“ |