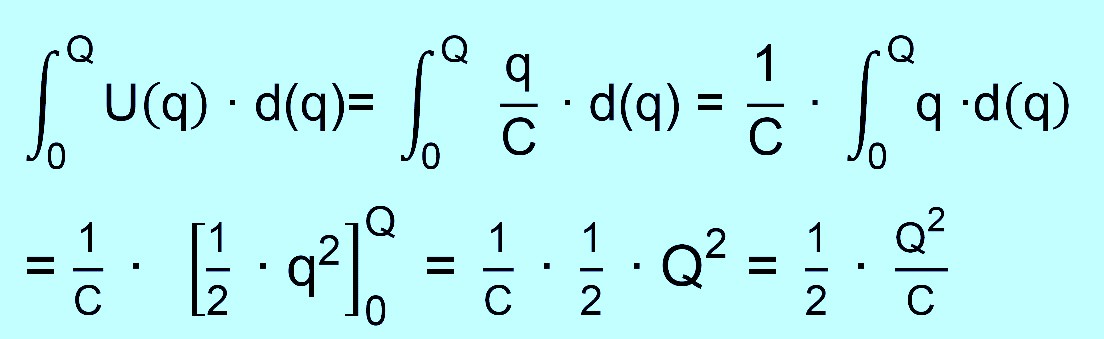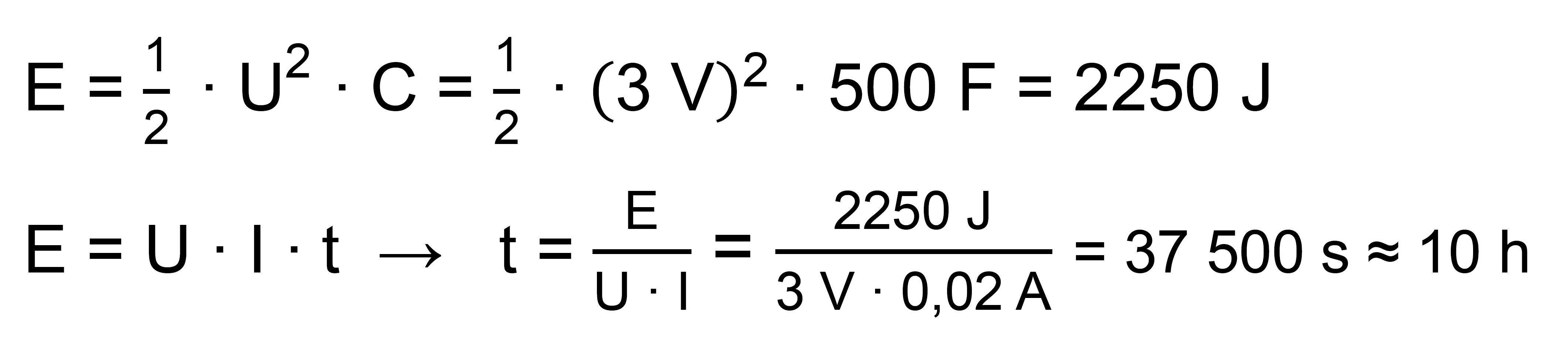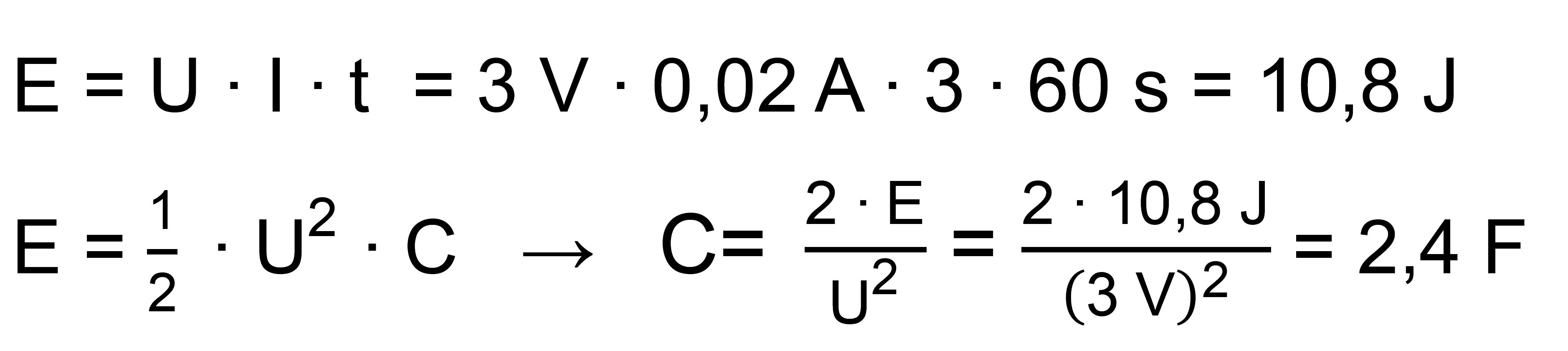|
Energie eines geladenen Kondensators Gedankenexperiment - Formel für die Energie Es
stellt sich zunächst einfach die Frage, warum ein geladener Kon- densator
eigentlich Energie gespeichert haben muss. Hierzu ein paar
einfache Überlegungen. Energie ist ja gespeicherte Arbeit, d.h. um einen
Kondensator zu laden, muss offensichtlich Arbeit verrichtet werden (s. Arbeit und
Energie). Wir
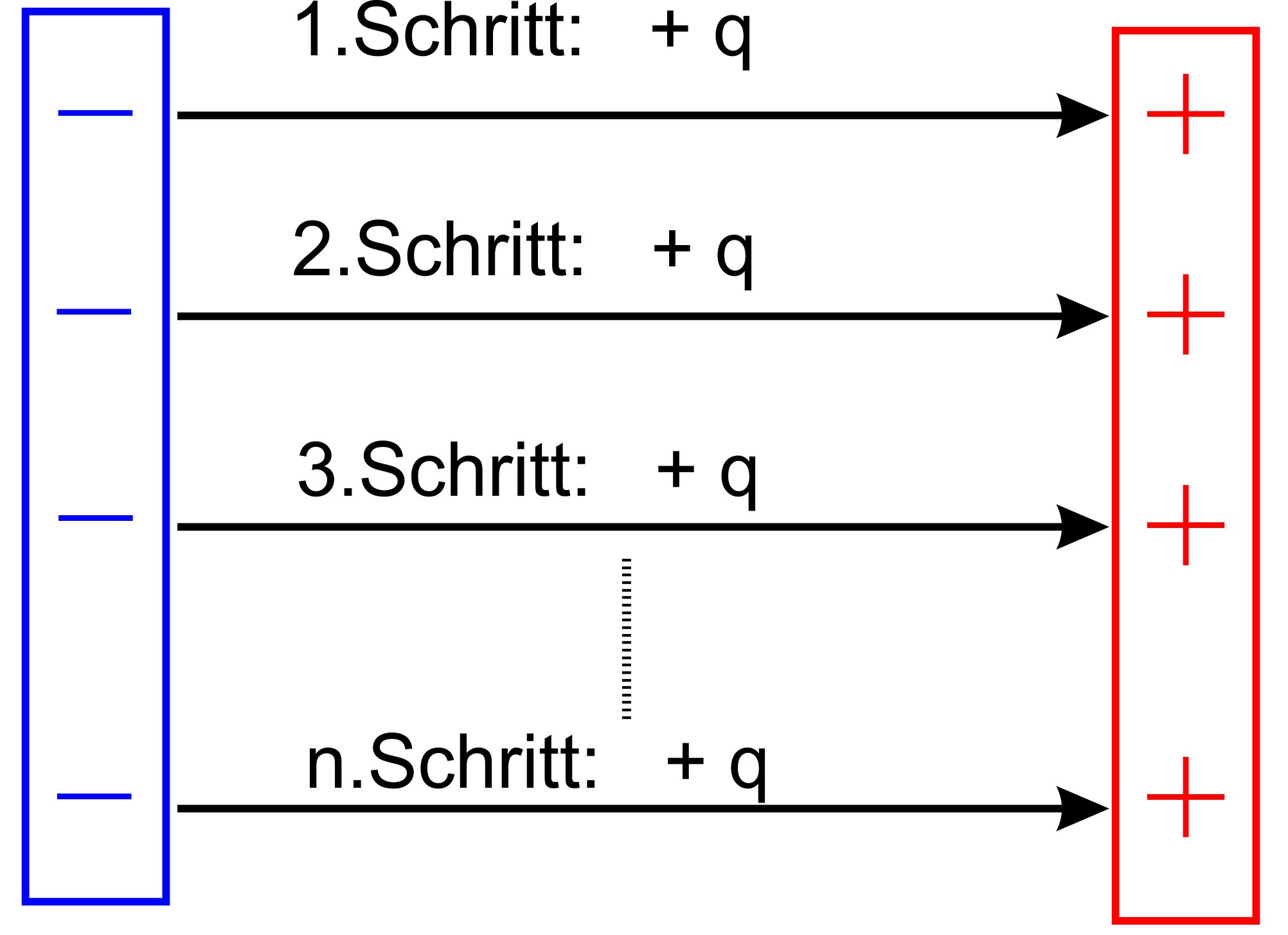
stellen uns dazu vor, die Ladungen wird schrittweise auf den Kondensator
aufgebracht, indem von der einen Platte des Kondensa- tors „per Hand“ immer eine Ladungsportion zur anderen
Platte trans- portiert
wird. Siehe hierzu folgende Abbildung:
Wir
beginnen bei einem neutralen (ungeladenem) Kondensator. Im
ersten Schritt wird eine Ladung +q von links nach rechts trans- portiert.
Hierzu muss keine Arbeit verrichtet werden, da ja noch kein
elektrisches Feld vorliegt bzw. keine abstoßende positive Ladung auf der
rechten Seite. Im zweiten Schritt wird ein weiteres +q nach rechts
gebracht. Diesmal liegt ein elektrisches Feld (bzw. eine Ab- stoßung
durch die im ersten Schritt transportierte Ladung) vor. Es wird Arbeit
verrichtet usw. Die verrichtete Arbeit pro transportierter
Ladung muss mit
jedem Schritt größer werden, da das E-Feld (bzw. die Ab- stoßung)
zunimmt. Wie
berechnet sich jetzt die pro Schritt verrichtete Arbeit? Wir leiten zunächst
eine allgemeine Formel für die Einzelschritte her und übertragen
diese dann auf jeden einzelnen Schritt. Für die
Arbeit gilt (s.
Arbeit):
für F
gilt: (s.
Feldstärke)
im homogenen Feld (gilt ja pro Schritt) ergibt sich
Man muss
jetzt alle Arbeiten aufaddieren und erhält dann die Gesamt- arbeit.
Dann müsste man noch eine Näherung für sehr kleine La-dungen
vornehmen. Am
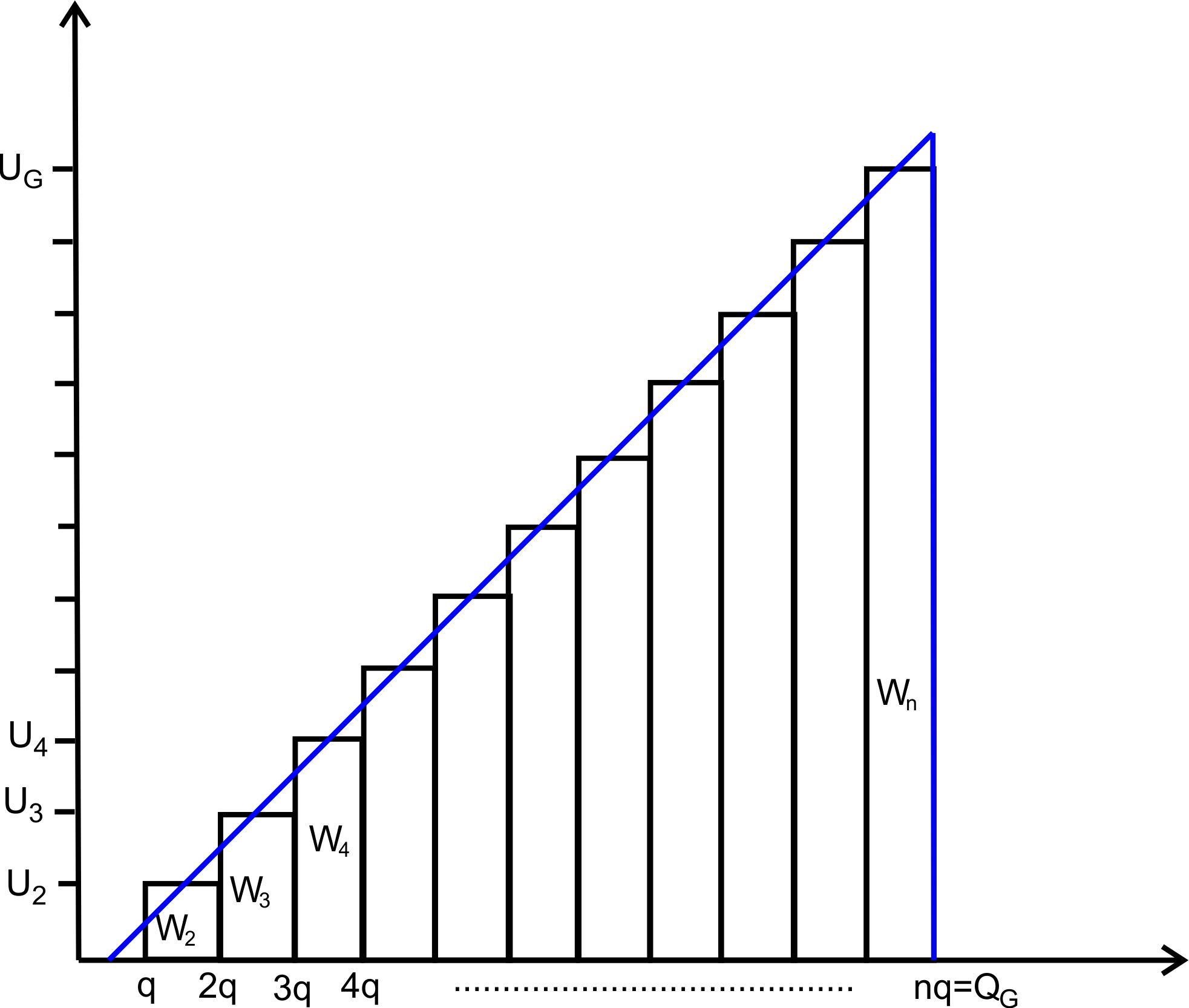
einfachsten schaut man sich das Ganze einmal graphisch an, in- dem man
ein Diagramm aufstellt, in dem die Spannung U gegen Q aufgetragen ist. Dies sieht in etwa folgendermaßen
aus:
Die
Fläche der Rechtecke entspricht der verrichteten Arbeit, da q ∙ U für die
Rechteckfläche gerechnet wird, d.h. die Gesamtfläche ergibt die
Gesamtarbeit. Für sehr viele kleine „q“-Werte (Näherung: n→∞) nähert sich diese Fläche immer mehr der Dreiecksfläche an, die durch die blaue Linie begrenzt wird. Die blaue Linie wird für sehr kleine q zu einer Ursprungsgeraden und endet bei UG. Somit ergibt sich für die Gesamtarbeit und damit die gespeicherte Energie die Formel:
Wir erhalten also als Formel für die im Kondensator
gespeicherte Energie.
1. Alternative: mathematische Formel-Herleitung
über das Integral Wenn schon genügend mathematischer Hintergrund vorliegt, kann man die Formel auch einfach mathematisch herleiten. Da die Fläche unter dem U-Q−Diagramm gefragt ist, kann man über die Integralrechnung die Formel erhalten. Das bestimmte Integral von 0 bis Q über den funktionellen Zusammenhang zwischen U und Q er- gibt ja die Fläche unter dem Graphen. U lässt sich aus der Ladung q einfach über die Funktion U(q) = q/C (s.o.) bestimmen. Die Herleitung geht dann so:
2. Alternative: mathematische Formel-Herleitung
über Gauß Wir haben oben gesehen, dass man die Einzelarbeiten aufaddieren muss. Es gilt dann also
Weiterführung zur Feldenergie Wenn man
weitere Umstellungen vornimmt, merkt man, dass die Energie
wohl im elektrischen Feld gespeichert ist. Man spricht dann von der
elektrischen Feldenergie. Die
Umstellungen gehen folgendermaßen:
Man hat
in der Formel nur noch „feldbeschreibende“ Größen, wie die Feldstärke
E und das Volumen V des Feldes. Daher wird häufig von Feldenergie gesprochen. Also ist die Energie nicht im
Kondensator gespeichert, sondern in seinem elektrischen Feld. Dies hat die
Kon-sequenz, dass, wenn es ein Feld ohne Kondensator gibt (z.B. elektro- magnetische
Wellen), auch Energiewerte vorliegen. Linkliste
zum Thema:
|