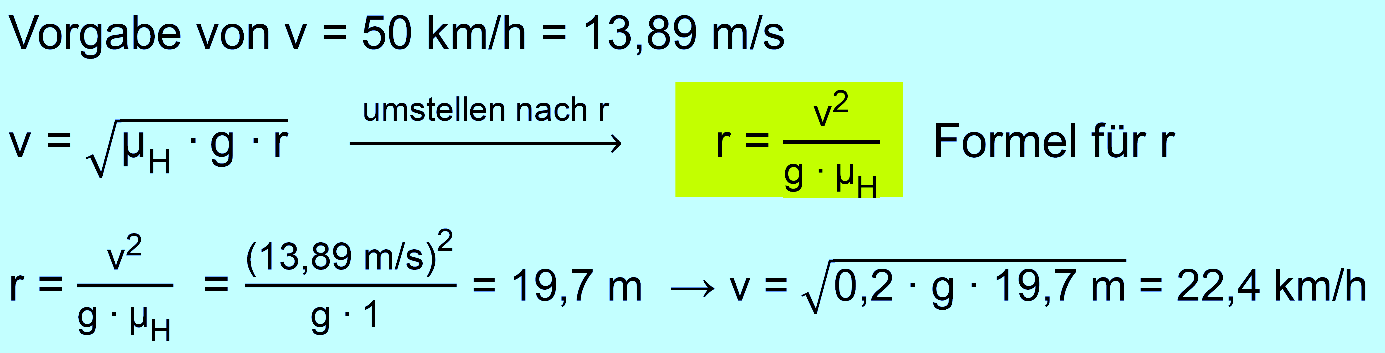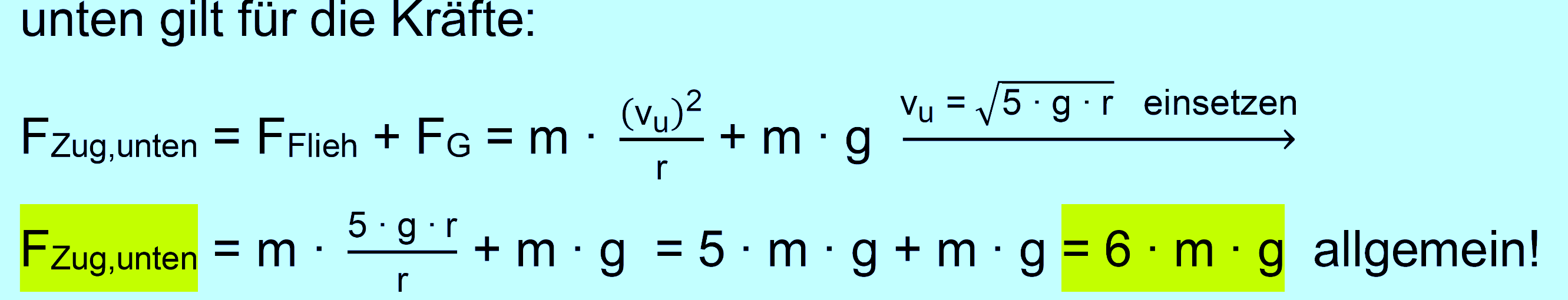|
Übungsaufgaben:
Kreisbewegung 1.
Übungsaufgabe: Kurvenfahrt PKW (mittel,schwer) Wir
betrachten die Kurvenfahrt auf einer normalen Straße (also nicht überhöht).
Die Kurvenfahrt soll auf einer Kreislinie mit dem Radius r
stattfinden. Bei Kreisbewegungen tauchen nach dem 1. Axiom von Newton
Trägheitskräfte auf. Hierzu kann man sich auch noch
einmal das Kapitel zur Fliehkraft anschauen. Um diese
Trägheitskräfte zu überwinden, muss eine Radialkraft (oder
Zentripetalkraft) auftreten, die den Körper auf die Kreisbahn zwingt. Bei
der Kurvenfahrt ist dies die Haftreibung der
Reifen. Diese
verhindert, dass der PKW einfach geradeaus fährt. Für die
Haftreibung gilt: FH
= µH ∙ FN
, wobei FN die Kraft ist, die senkrecht zur
Oberfläche wirkt, also in
unserem Fall die Gewichtskraft FG. µH ist der Haft- reibungskoeffizient, der von vielen Bedingungen abhängt und in Tabellen
nachgeschlagen werden muss. Jetzt zur
eigentlichen Aufgabe: a.) Wir wollen
für zwei Kurvenradien und unterschiedliche Straßenverhältnisse
einmal die Maximalgeschwindigkeit für das Durchfahren
der Kurve berechnen. r1
= 150 m, r2 = 15 m (Serpentine) trockene
Asphalt: µH = 1,0 nasser
Asphalt: µH = 0,8 vereiste
Fahrbahn: µH = 0,2 (Hinweis: Ich beziehe mich bei den Werten für µH auf den
Artikel bei technikmathe.de) b.) In
geschlossenen Ortschaften darf man üblicherweise maximal mit 50 km/h fahren.
Wie groß darf der Kurvenradius sein, wenn man in einer
geschlossenen Ortschaft bei trockenem Asphalt mit 50 km/h durch
die Kurve fahren will. Welche Geschwindigkeiten müssen in
dieser Kurve eingehalten werden, wenn die Straße vereist ist? Lösung: Es gilt:
zu b.)
Links
zur Aufgabe:
Für die
folgenden Übungsaufgaben sollte man das Kapitel: Besondere Kreisbewegungen unbedingt
durchgelesen haben. 2.
Übungsaufgabe: Kirmes-Enterprise (mittel) Im Video
sieht man das Fahrgeschäft „Enterprise“.
Das habe
einen Radius von 10 m und laufe mit 15 Umdrehungen pro Minute (s.
hierzu Link: Enterprise bei wikipedia). a.)
Bestimmen Sie die g-Kräfte am oberen und unteren Punkt der Kreisbahn. b.)
Berechnen die Anzahl der Umdrehungen, damit am oberen Punkt
Schwerelosigkeit vorliegt. Lösung: a.) Für die Kräfte gilt:
b.)
Hinweis:
Für diese Aufgabe wird auch der Energieerhaltungssatz benötigt. 3.
Übungsaufgabe: vertikaler Fadenkreis (mittel, schwer) An einer
Schnur wird auf deinem vertikalen Kreis eine Masse m herumgeschleudert.
Der Radius der Kreisbahn betrage r = 1,2 m. a.) Welche
Geschwindigkeit muss die Masse am oberen Punkt aufweisen,
damit die Zugspannung 0 N beträgt, d.h. die Masse sich so
gerade kreisförmig bewegen lässt. b.) Zeigen
Sie allgemein, dass wenn oben die Zugspannung 0 N beträgt,
dass dann unten eine Zugspannung von 6 ∙ FG wirkt. Lösung: a.) +
b.)
4.
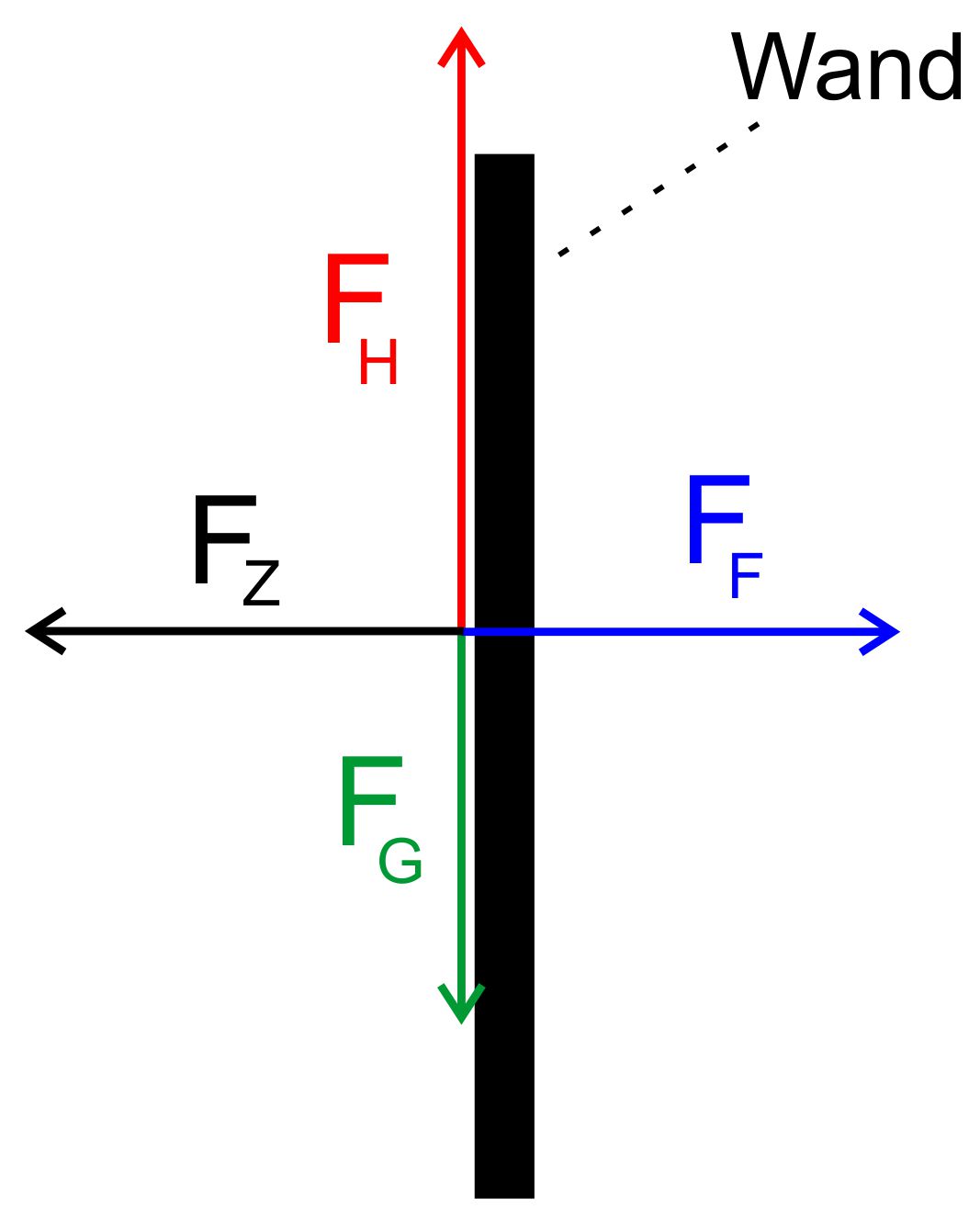
Übungsaufgabe: Rotor, Round Up, Waschmaschine Bei dem
Fahrgeschäft „Rotor“ werden Personen in einer Trommel durch
schnelle Rotation an die Wand gedrückt (s. Video) Quelle(Ausschnitt): Cousin
Freaks auf ROTOR - YouTube Über die
Abmessungen gibt es unterschiedliche Angaben. Mir scheinen beim
Blick auf das Video folgende Maße vernünftig zu sein:
Durchmesser 4,6 m; Umdrehungsfrequenz 28 Umdrehungen pro Minute.
Mit diesen Werten soll hier gerechnet werden. a.) Geben
Sie alle Kräfte an, die auf die Person einwirken. Welche
Kräfte sind dafür verantwortlich, dass die Personen an der Wand
haften? Welche Bedingungen müssen dafür erfüllt sein? b.) Wie
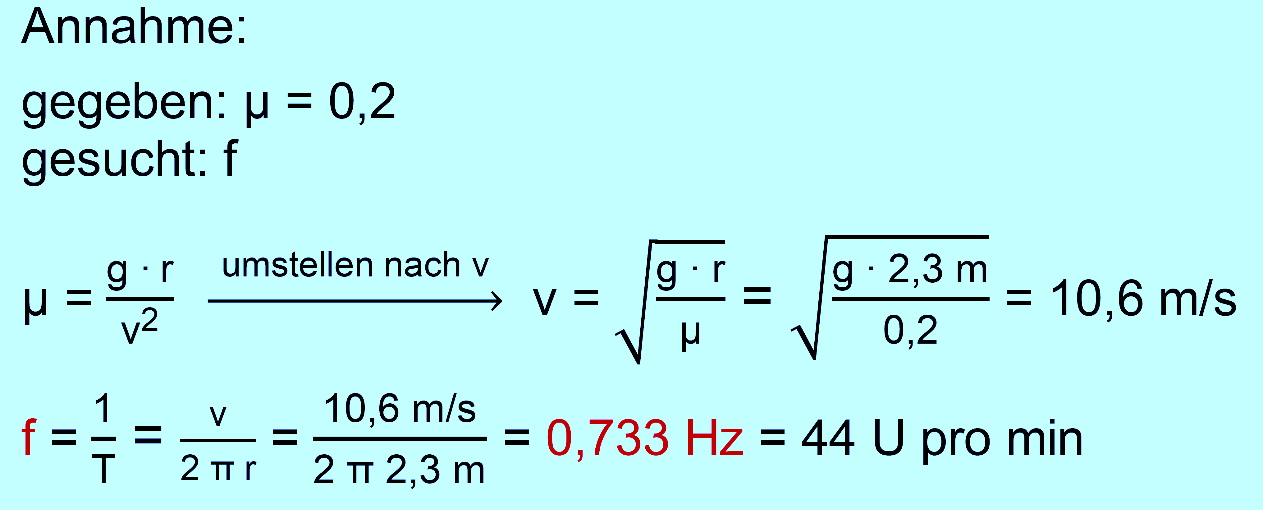
groß muss bei den obigen Angaben der Haftreibungs- koeffizient
sein, damit die Personen an der Wand „kleben“ bleiben? c.) In
manchen Quellen wird von Haftreibungskoeffizienten der Größe 0,2
ausgegangen. Diese Personen würden bei den obigen Maßen
abrutschen. Wie groß müsste die Umlauffrequenz sein, damit dies
gerade nicht passiert? d.) Beim Round
Up haben wir größere Maße vorliegen. Außerdem kann der
Aufbau geschwenkt werden. Im Huracan (Heidepark) liegen die
Maße bei: Durchmesser 9 m, Umlauffrequenz 18 Um- drehungen pro
Minute. Könnte man hier die Personen (wie in der Enterprise)
auf einem vertikalen Kreis rotieren lassen? e.) In
einer Waschmaschine hat die Wäschetrommel einen Durch- messer von
ca. 50 cm und kann im Schleudergang mit bis zu 1400 Umdrehungen
pro Minute rotieren. Welche G-Werte treten hier auf? Lösung: a.) Die Kräfte sind in folgender Abbildung eingetragen.
zu b.)
zu c.)
zu d.)
zu e.)
5.
Übungsaufgabe: Kettenkarussell Bei unseren
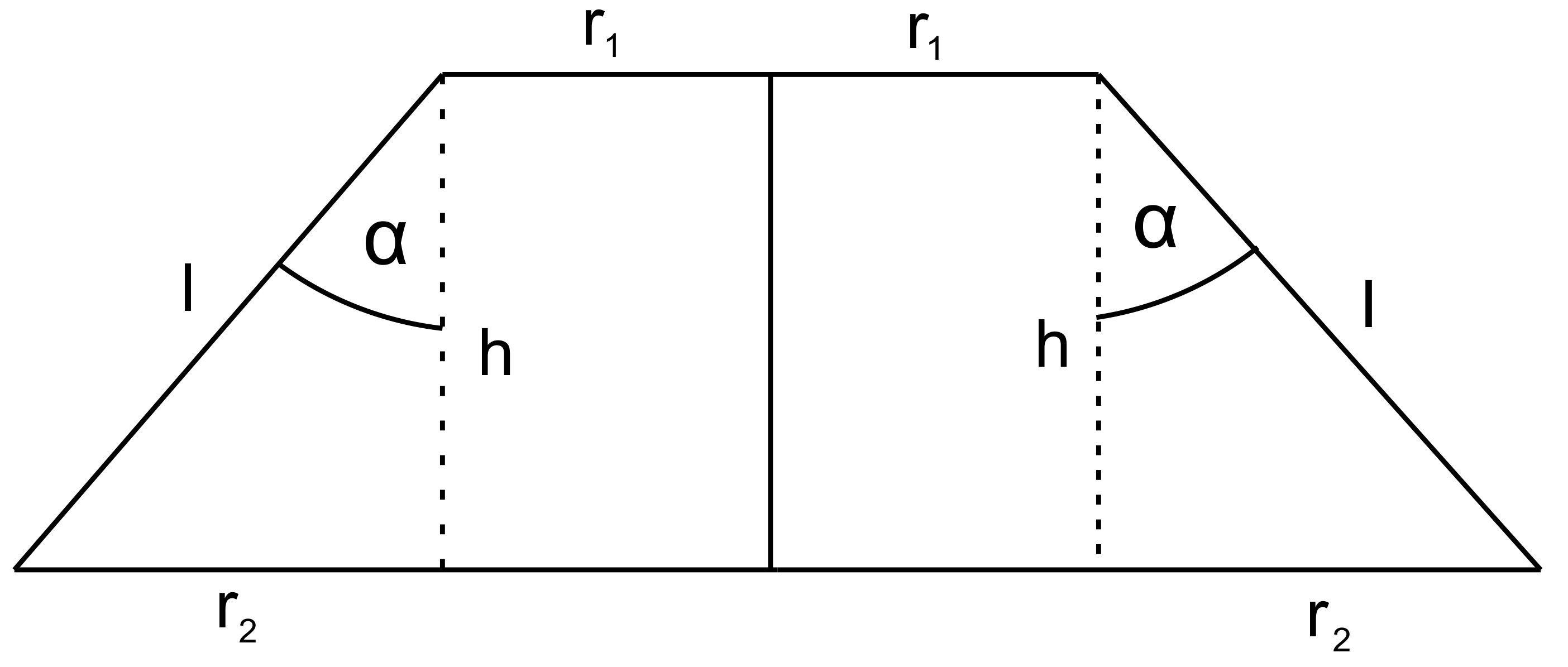
Betrachtungen zum Kettenkarussell gehen wir von einem trapezförmigen Aufbau
aus. (s. Abbildung).
mit l = Kettenlänge; r1 = Radius der oberen
Aufhängung; r1+r2 = Radius der Flugbahn; α =
Neigungswinkel = Winkel zwischen Kette und Vertikaler Es ist
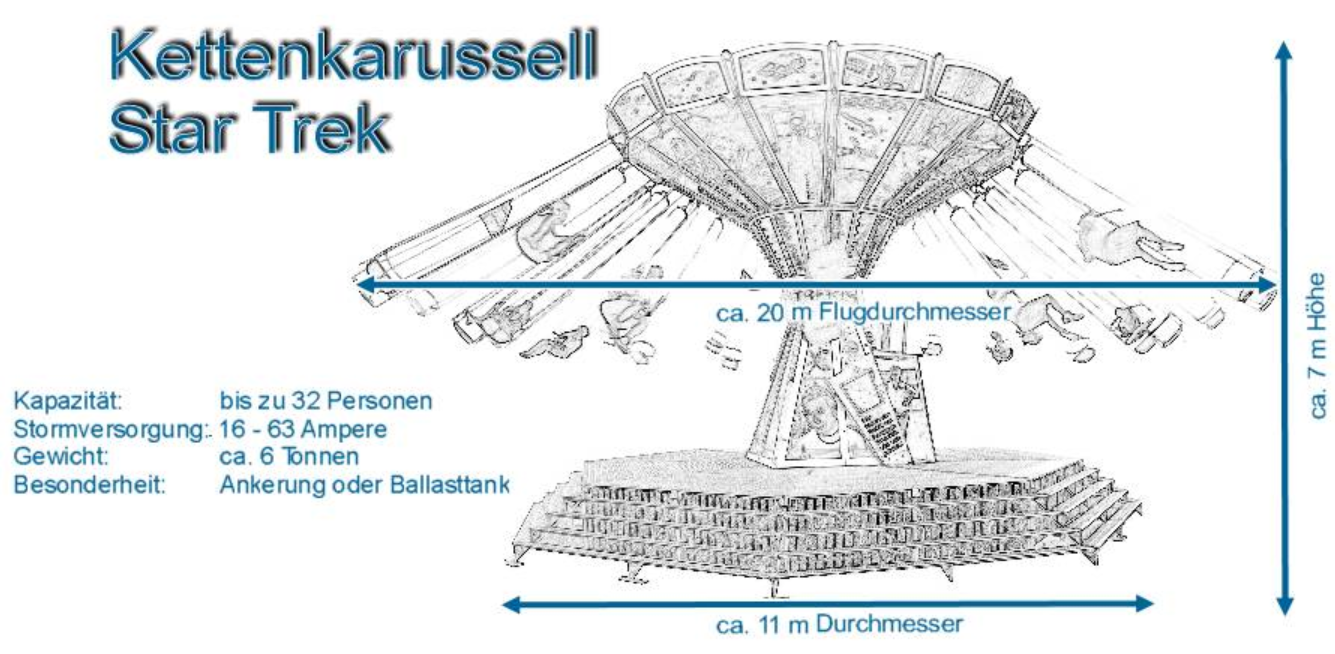
ziemlich schwierig Maße von solchen Kettenkarussells im Internet zu
finden Ein Skizze habe ich vom Modell „Star Trek“ ent- deckt. (s.Abb.).
Quelle: https://musiolek.com/vermietung/fahrgeschaefte/kettenkarussell Hieraus ergeben
sich für mich durch Abmessen und Abschätzen folgende
Maße für das Trapez: r1 = 3 m; r1+r2 = 10 m;
h = 5 m a.)
Bestimmen Sie hieraus die Geschwindigkeit des Karussells! Für das
Modell „Wellenflug“ habe ich die meisten Angaben auf
diesem
Link gefunden. Man findet: v = 30
km/h; α = 44°; l = 7 m b.) Bestimmen
Sie hieraus die Länge der Strecke r1. Lösung: Hinweis:
α im Kapitel „besondere
Kreisbewegung“ ist der andere Winkel. zu a.)
zu b.)
- zurück zum Kapitel „Kreisbewegungen“ - weiter zur
Übersicht zum Thema „Arbeit und Energie“ |