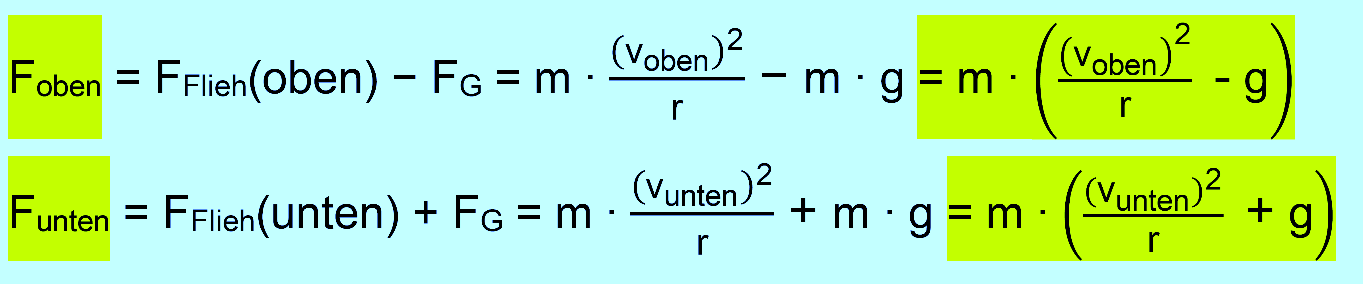|
- Kräfte auf Insassen
- Geschwindigkeit
- Mindesthöhe
- Klothoide Physik
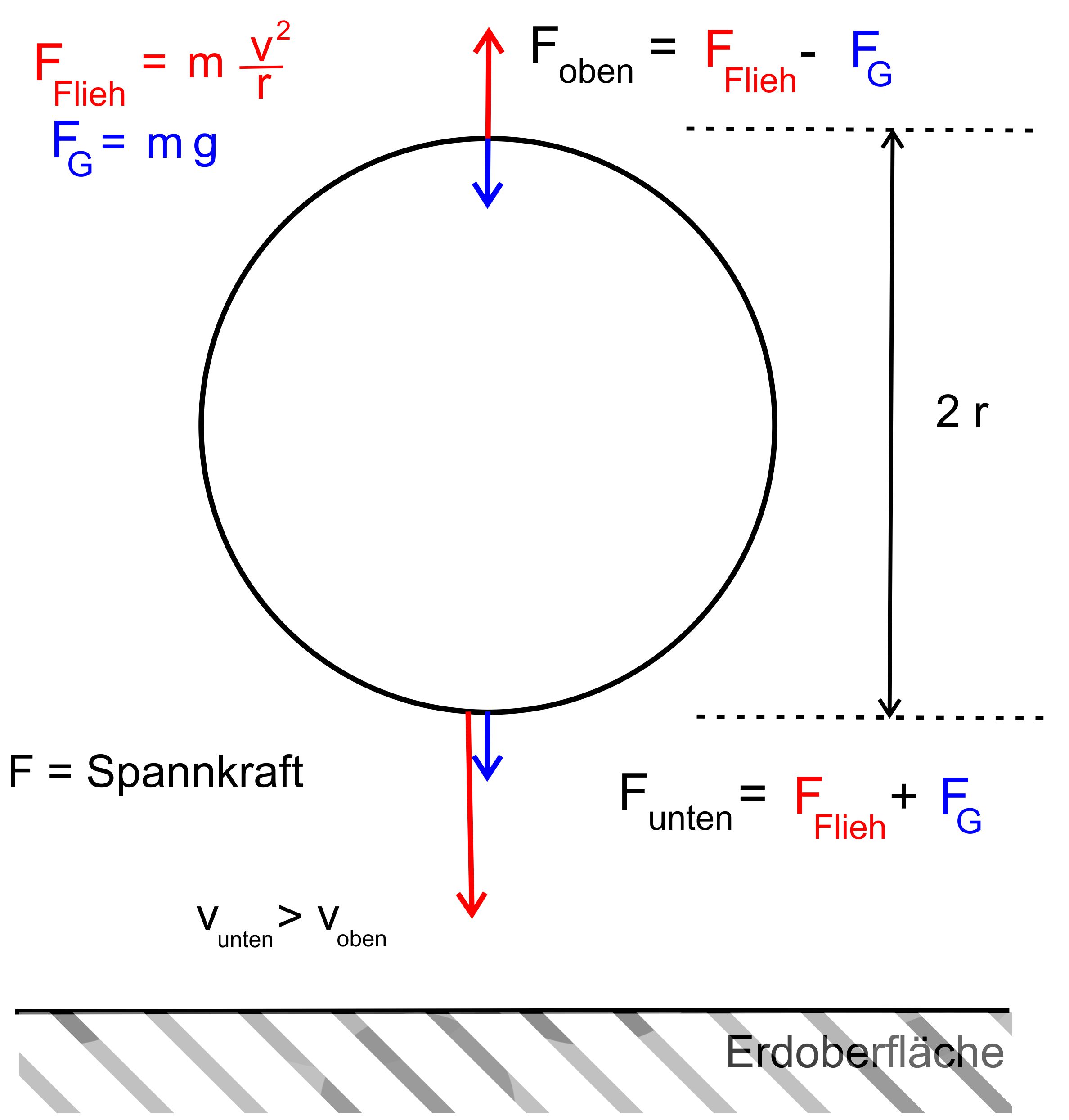
zum Looping Allgemeine Bemerkungen Auf dieser Webseite gibt es mehrfach Betrachtungen zum Looping: - allgemeine Überlegungen (vertikaler Kreis) - Übungsaufgaben 1 Kreisbewegungen (Aufgabe Nr.2 + Nr.3) - Übungsaufgaben 2 Kreisbewegungen (Aufgabe Nr.2 + Nr.3) - Klausuraufgaben Energieerhaltungsatz (Aufgabe Nr.2) Es bietet sich daher an, sich noch einmal ausführlicher mit diesem Achterbahnelement zu beschäftigen. Definition: Unter dem Looping versteht man bei der Achterbahn eine „vertikale Krümmungsform“, die die Besucher über Kopf durch- fahren. Looping in Kreisform Beim Looping in Kreisform geht es um die Physik des vertikalen Kreises. Hierzu gelten folgende Verhältnisse für die Kräfte, die auf die Insassen der Wagen wirken (s. Abb. aus vertikaler Kreis)
Es gilt:
Man sieht, dass sich unten die Kräfte addieren. Da unten auch deutlich größere Geschwindigkeiten vorliegen (s.u.), ergeben sich im unteren Teil des Loopings deutlich größere Kräfte als am oberen Punkt. 2. Geschwindigkeiten im Looping Da im Looping natürlich auch der Energieerhaltungssatz gilt, muss im oberen Punkt die gleiche Energie wie im unteren Punkt vor- liegen. Die Gesamtenergie ist dem System durch den Start („Lift- hill → potentielle Energie“ oder durch ein „Katapult → kinetische Energie“) vorgegeben worden. Im oberen Punkt gibt es sowohl potentielle als auch kinetische Energie. Im unteren Punkt nur kinetische Energie, falls der untere Punkt auf Nullniveau für die potentielle Energie liegt (z.B. h = 0 m). Es gilt also:
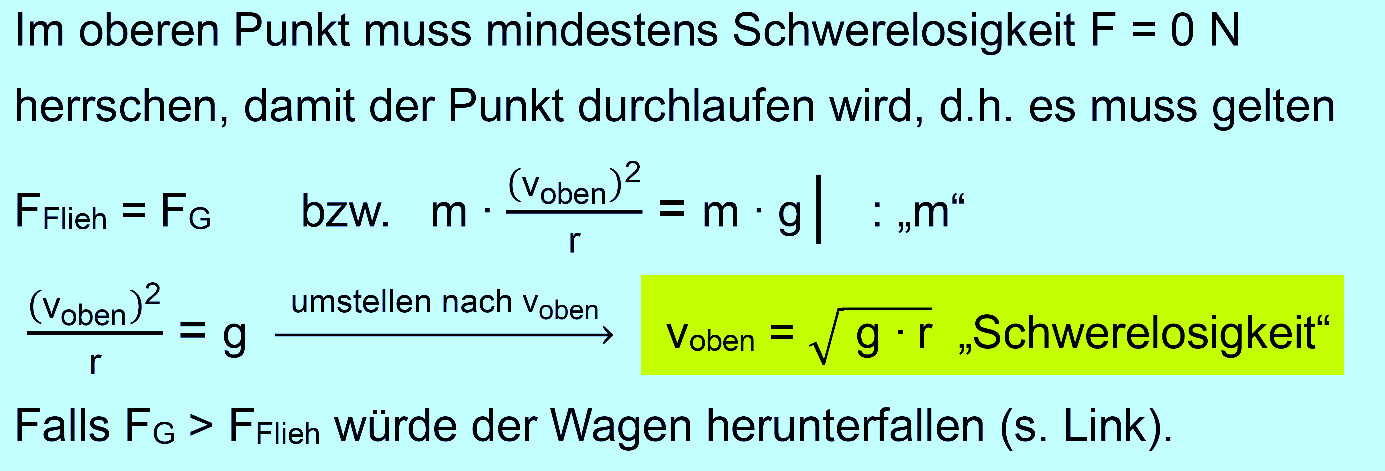
Die Geschwindigkeit unten ist also deutlich höher als die Geschwin- digkeit im oberen Punkt. Was bedeutet dies jetzt für die Kräfte bzw. G−Werte? Link: eine konkrete Rechnung gibt es hier für den Fall,
dass oben Schwerelosigkeit herrscht.
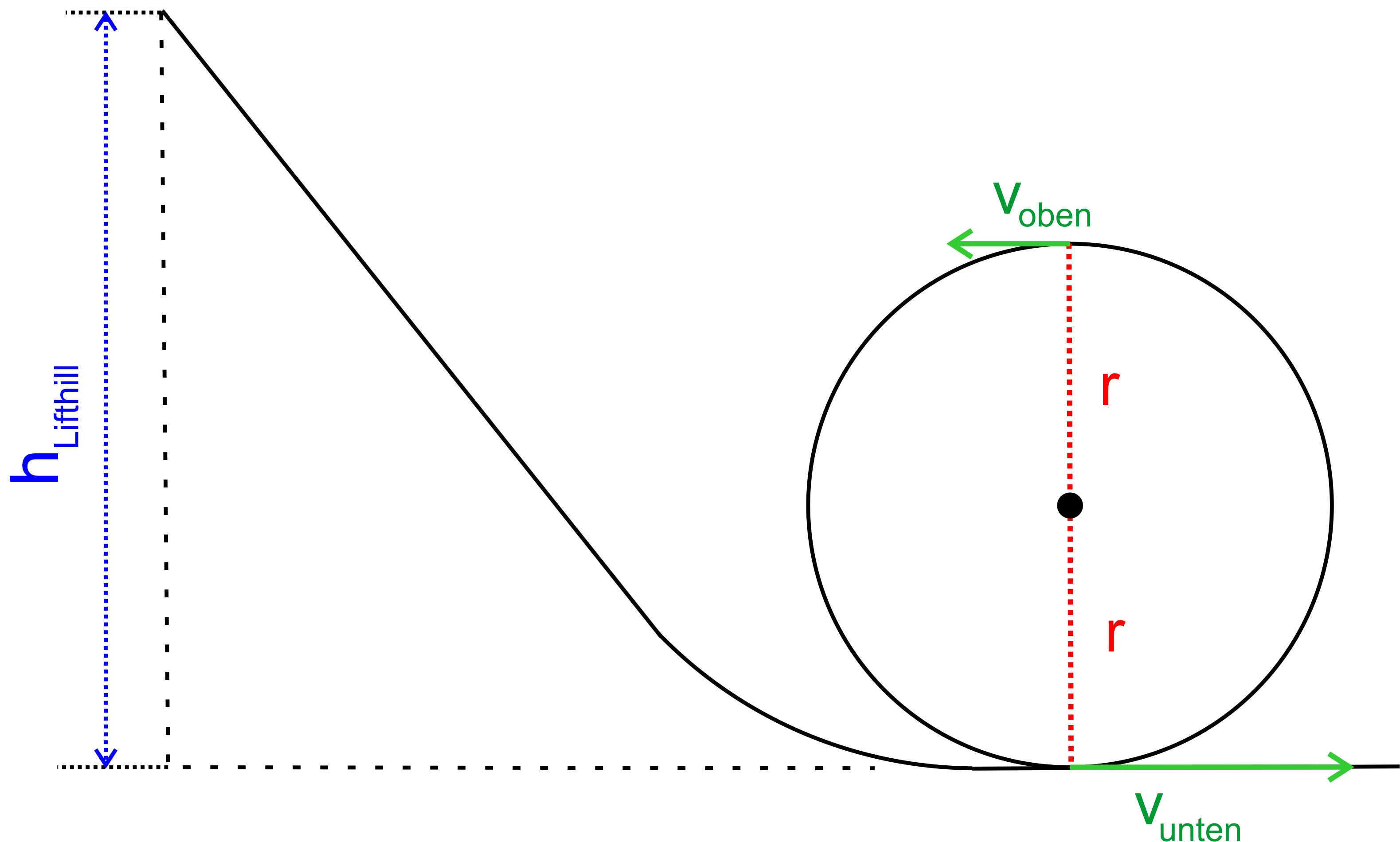
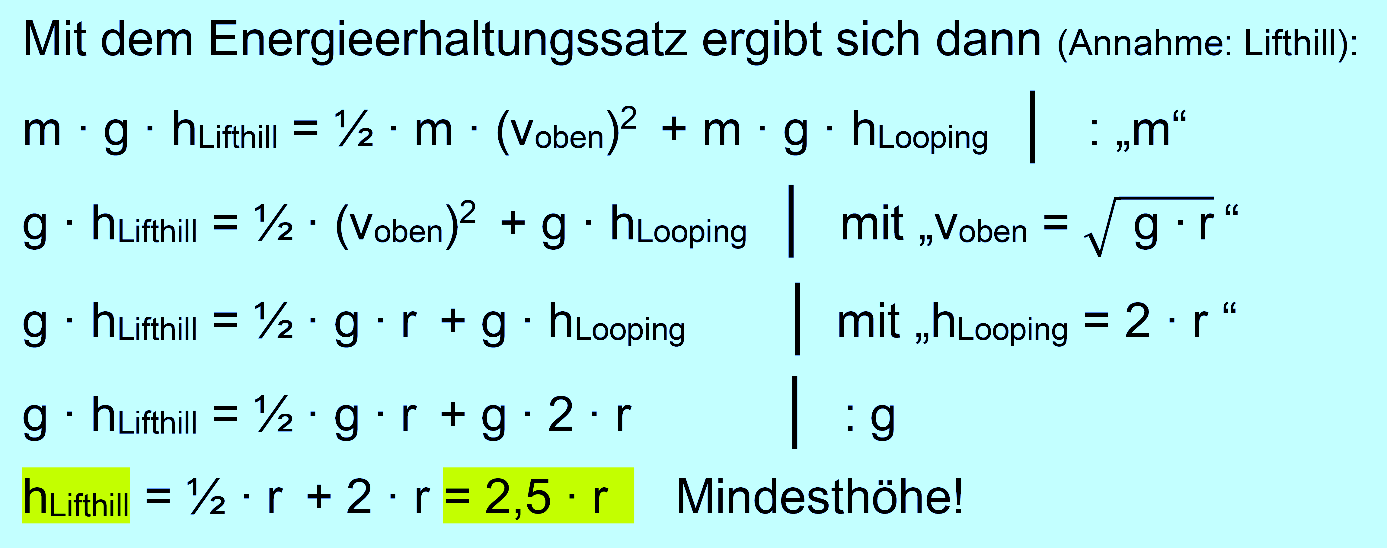
3. Mindesthöhe (Lifthill) für Looping-Durchlauf Um einen Looping zu durchfahren, braucht es einer Mindestanfangs- höhe, von der aus die Wagen starten. Diese Mindesthöhe lässt sich recht einfach mit Hilfe des Energieerhaltungssatzes bestimmen. Zur Veranschaulichung der Größen soll zunächst eine Abbildung dienen.
Es gilt nun:
Die Mindesthöhe muss also „ 2,5 ∙ r “ betragen. Was bedeutet dies für
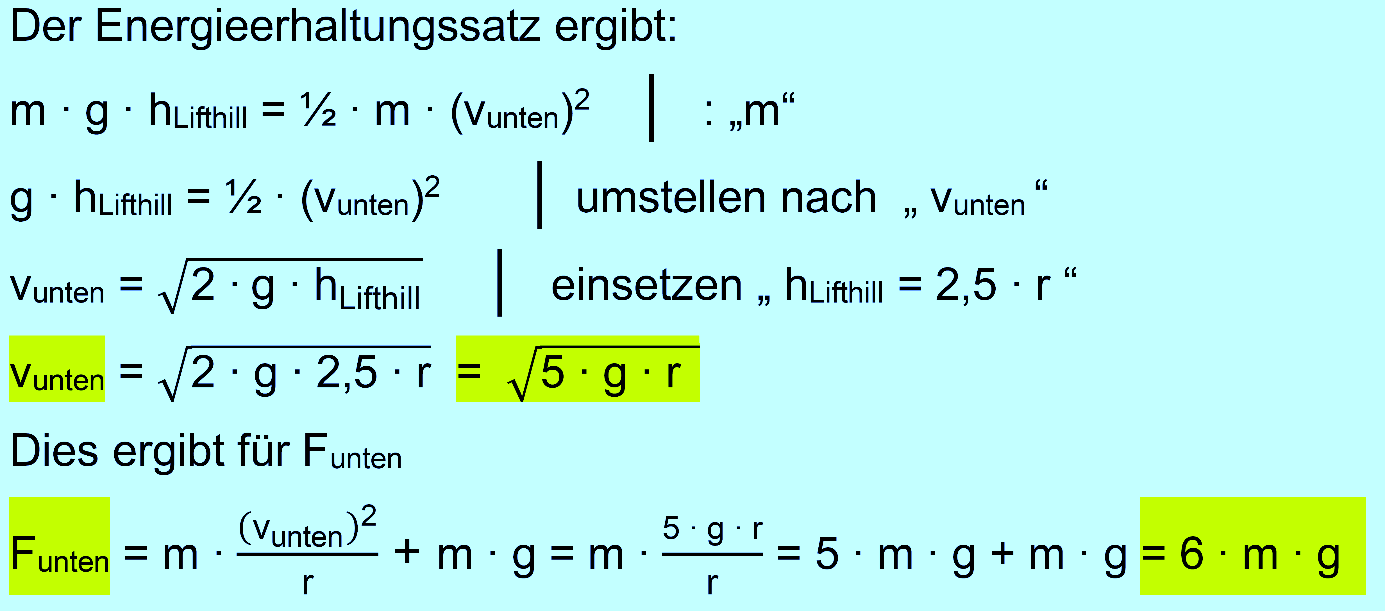
die Kraft, die die Insassen unten in die Sitze drückt?
Das Ergebnis ist eigentlich nicht überraschend, da wir ja schon im 2. Kapitel gezeigt haben, dass sich die Kraft am unteren Punkt ergibt, in dem man zur oberen Kraft „ 6 ∙ m ∙ g “ hinzu- addiert. Wichtiges Ergebnis: Selbst unter den günstigsten Verhältnissen (nur
Mindesthöhe) wird man mit F = 6 ∙ m ∙ g, also 6−fachem
Eigengewicht in die Sitze gepresst. Dies kann schon zu Gesundheitsschäden führen (s.
Linkliste). Daher werden praktisch keine kreisförmigen Loopings
mehr gebaut. Die Achterbahn Flip Flap
war die erste, die überhaupt mit einem Looping gebaut wurde. Der Looping hatte damals
Kreisform und es traten Kräfte von bis zu 12 g auf, so dass die
Achterbahn wegen der gesundheitlichen Probleme der Insassen, schnell
wieder abgebaut wurde. In neuster Zeit gab es noch die Achterbahn
„Thriller“ von Schwarzkopf, die sogar 4 kreisförmige Loopings
aufwies, wobei eine Krafteinwirkung bis 6,5 g möglich war. Aber
auch diese Bahn ist inzwischen verschrottet. Looping
in Klothoidenform Werner Stengel, der Ingenieur für Achterbahnen, kam
im Jahr 1976 auf die Idee die Kreisform durch eine Klothoide zu ersetzen.
Diese Form wurde schon früh (1937) im Strassenbau
eingesetzt, um einen allmählichen Übergang bei der Kurvenfahrt zu
erreichen, damit das Lenkrad nicht „abrupt“ herumgerissen
werden musste. Den starken Einfluss von Werner Stengel
auf den Achterbahnbau erkennt man daran, dass sein Büro inzwischen über
700 Achter- bahnen weltweit konstruiert hat Der Vorteil der Klothoide ist, dass der Radius
allmählich kleiner wird. Man hat zunächst große Radien, die mit der Länge der
Linie immer kleiner werden. Oder mathematischer ausgedrückt: der
Krüm- mungsradius
r verhält sich umgekehrt proportional zur Bogen- länge r = c ∙ 1/b (r = Radius, b = Bogenlänge, c = Konstante). Hinweis: Wir können im Rahmen
dieser Webseite, die sich mit Oberstufenphysik beschäf- tigt, nur sehr allgemeine Betrachtungen
zur Klothoide abgeben. Wer eine ausführlichere Betrachtung wünscht, sollte sich
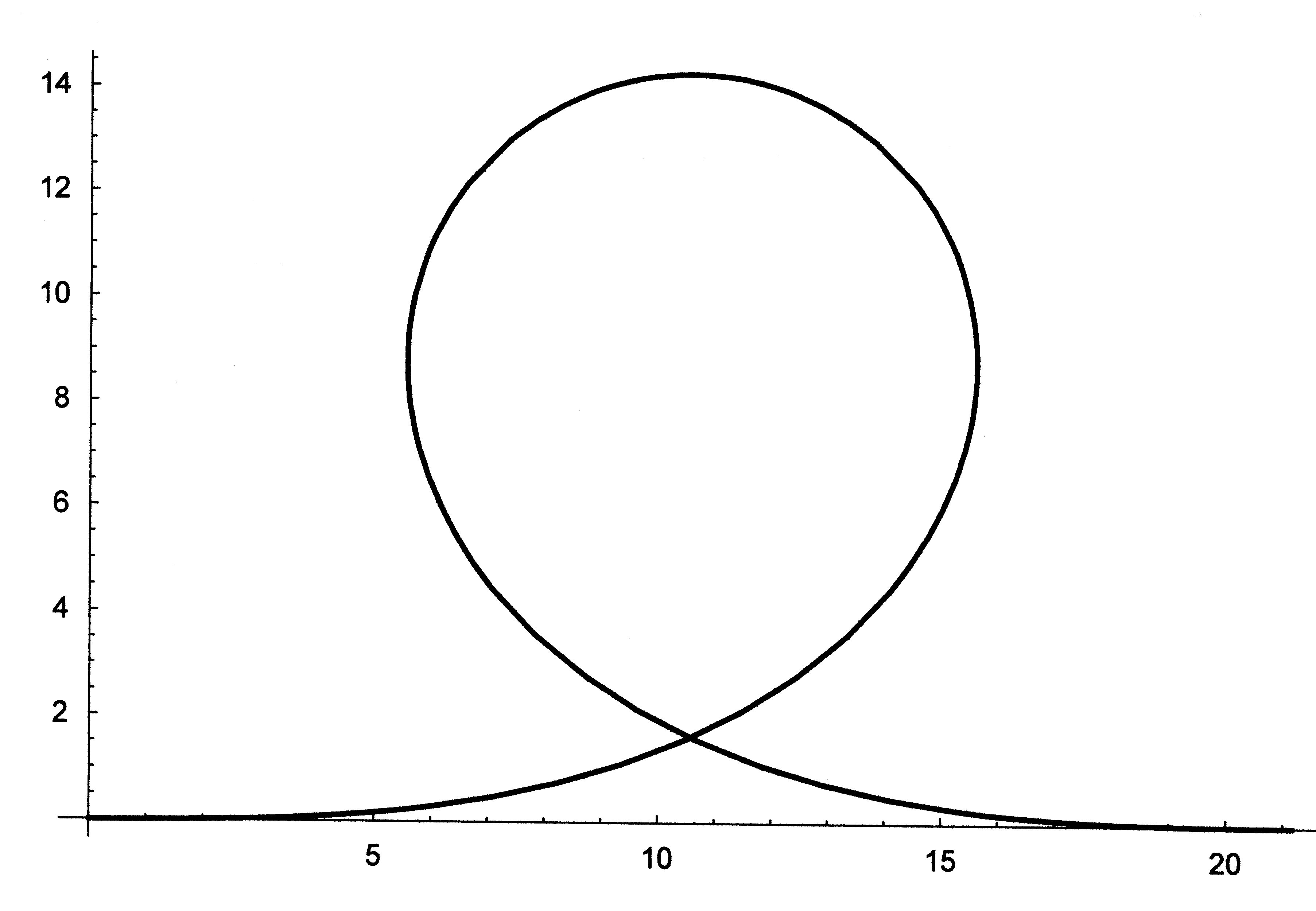
das Buch von Rainer Müller zur Hand nehmen. ( s. Linkliste) In der folgenden Abbildung ist einmal eine Klothoide
abgebildet, die für einen Looping von 14 m Höhe zutrifft, den
man z.B. beim „Looping Star“ findet. Hinweis: Rechnungen zum Looping
Star findet man
unter
diesem Link.
Hinweis: der Programmcode für die
Darstellung der Klothoide mit mathematica ist in der Linkliste aufgeführt. Man erkennt gut die allmähliche Änderung der Krümmung zu kleineren Radien. Kleinere Radien bedeuten ja größere Fliehkräfte, da Fz = m ∙v2/r gilt. Also hat man zunächst geringe Fliehkräfte, die
dann immer mehr zunehmen, da r kleiner wird. Dem entgegenwirkt
allerdings die Abnahme der Geschwindigkeit wegen der Zunahme
der potentiellen Energie. Dies geht sogar quadratische
ein. Also wird irgendwo zwischen dem unteren und dem
oberen Punkt der Klothoide die Stelle sein, an der die G-Kräfte
am größten sind Diese sind damit auch deutlich kleiner als bei
einer Kreisform. In den folgenden Abbildungen aus dem Buch von Rainer
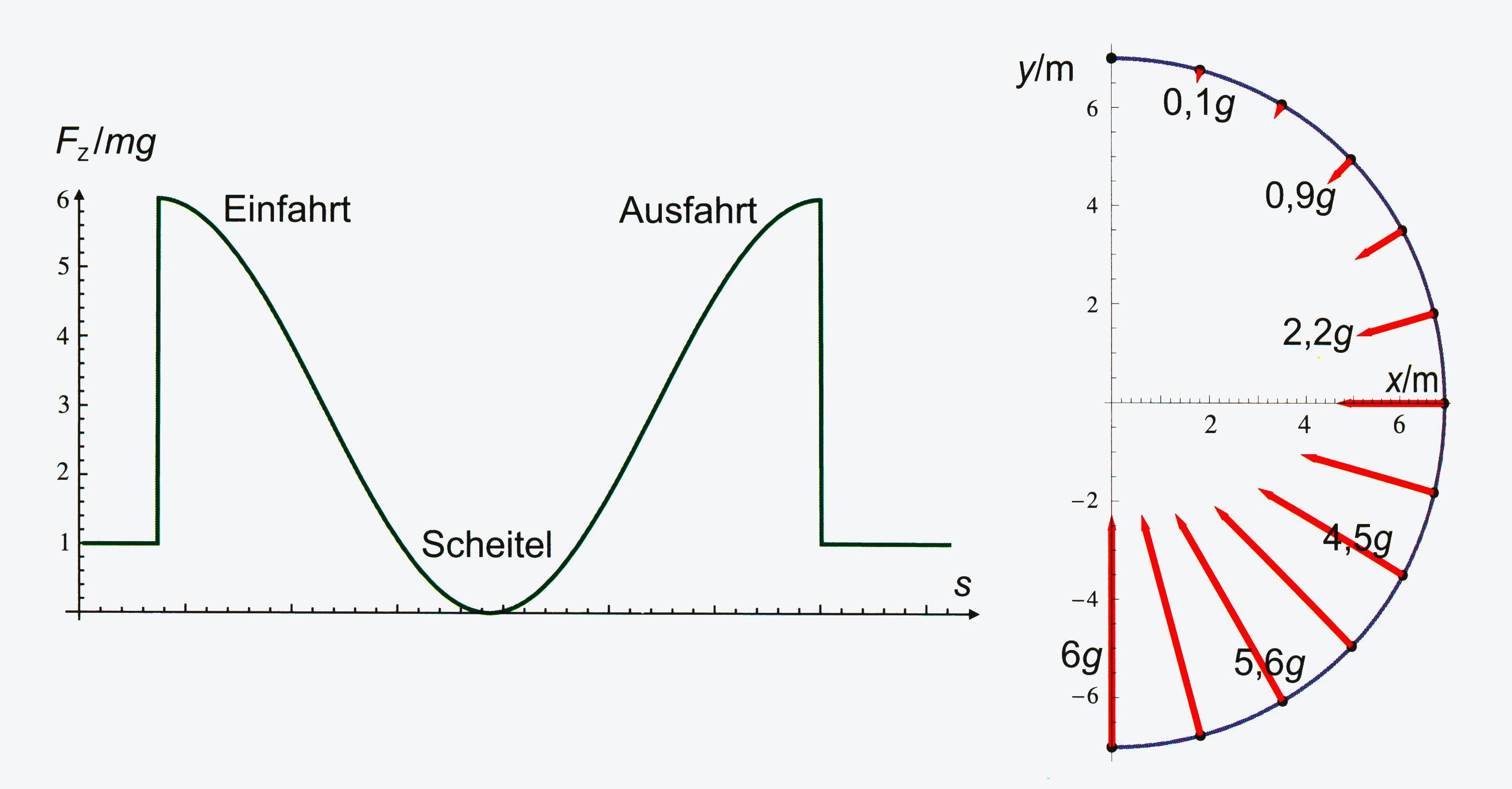
Müller werden die Verhältnisse einmal vergleichen. 1. G-Werte beim Kreisbogen
2. G-Werte bei der Klothoide
Quelle:
Rainer Müller, Klassische Mechanik Abb.14.24 bzw. Abb.14.31; Genehmigung
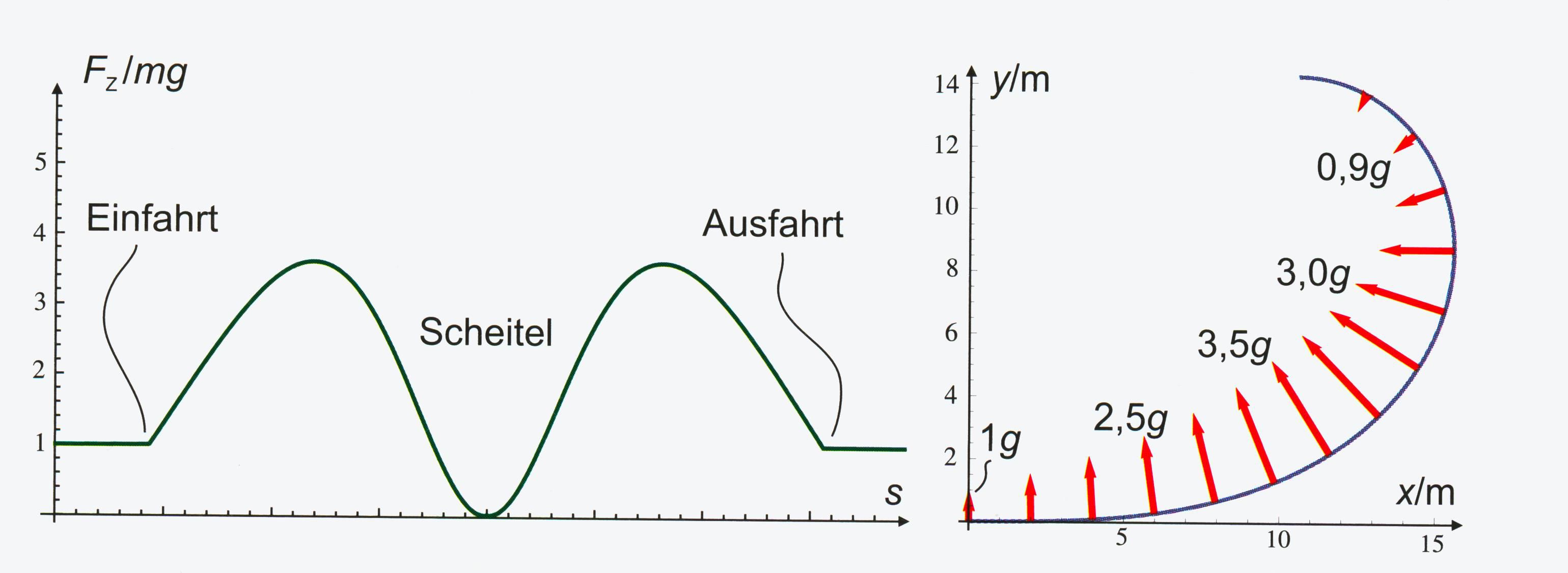
zur Veröffentlichung liegt vor Bei der Kreisform ist die Zunahme der G-Kräfte
abrupt, von 1g bei der Anfahrt zu 6 g bei der Einfahrt. Dann nehmen die
G-Kräfte all- mählich ab, da v abnimmt, r bleibt allerdings
konstant. Bei der Klothoide nehmen die G-Werte allmählich zu,
um dann mit 3,5 g den höchsten Wert schon im unteren Bereich der
Klothoide zu erreichen. Danach nehmen die Werte bis zum oberen
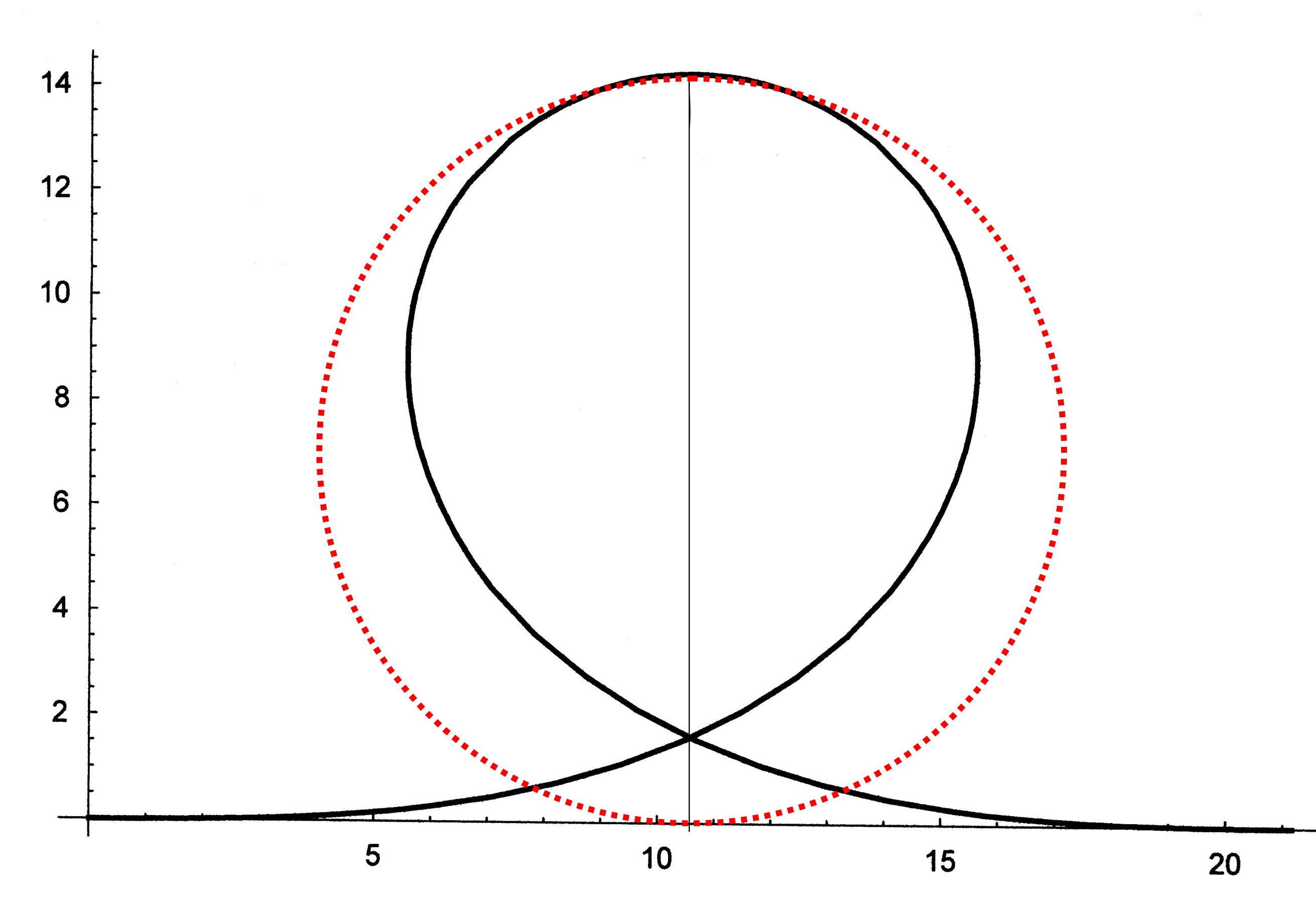
Punkt ab. Am Schluss noch eine Abbildung, bei der man noch
einmal den Konstruktionsunterschied zwischen Klothoide
(schwarz) und Kreisform (rot) erkennen kann.
Hier noch einmal in Natura ein Vergleich zwischen
Kreisform und Klothoide. (Quelle: Michael Pantenburg;
https://www.schwarzkopf-coaster.net/hauptmenueGF.htm)
Linkliste:
Sprung zu - Kräfte auf Insassen - Geschwindigkeit - Mindesthöhe - Klothoide - Besondere
Kreisformen (vertikal, horizontal) -
Übungsaufgaben Kreisbewegung 1 - Übungsaufgaben
Kreisbewegung 2 -
Klausuraufgaben Energieerhaltung |