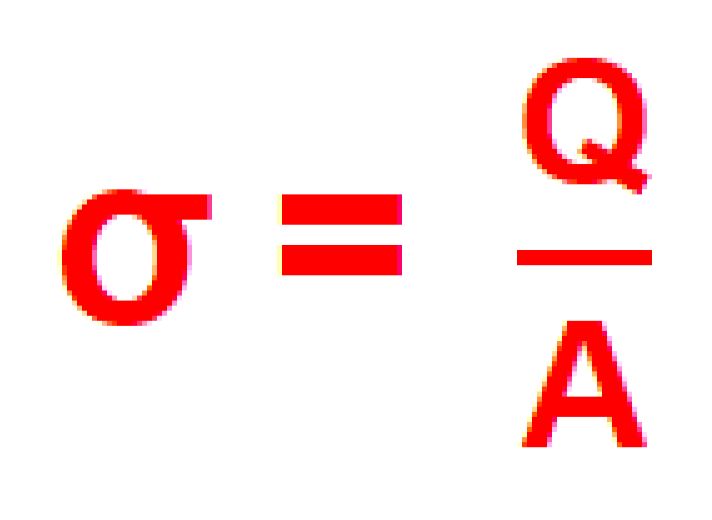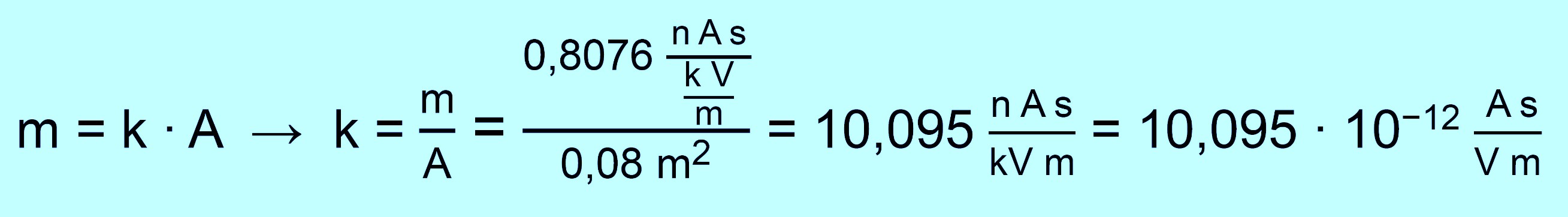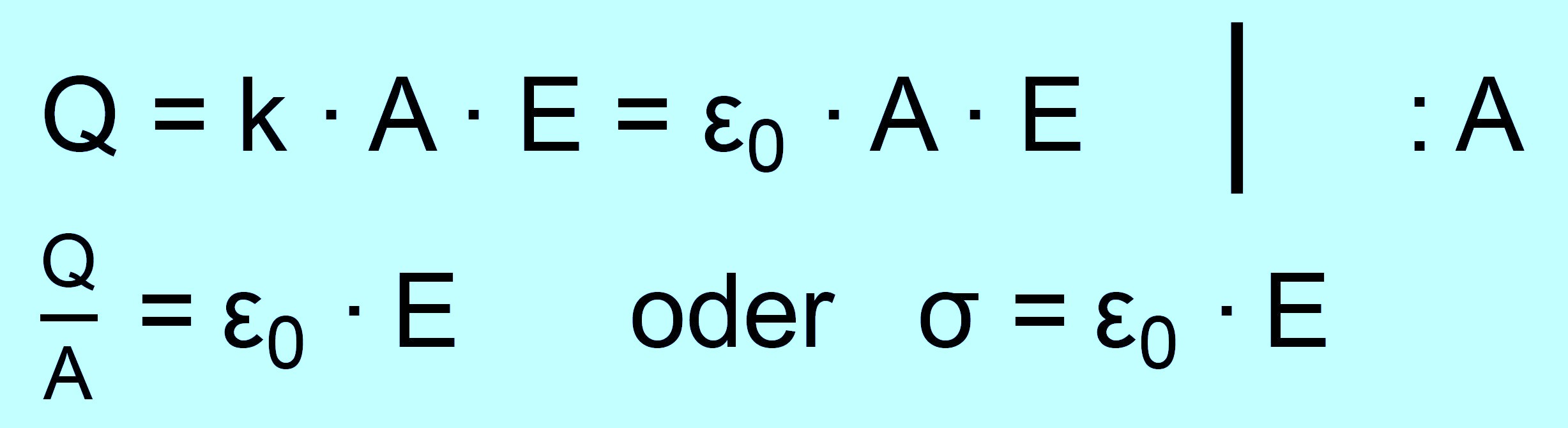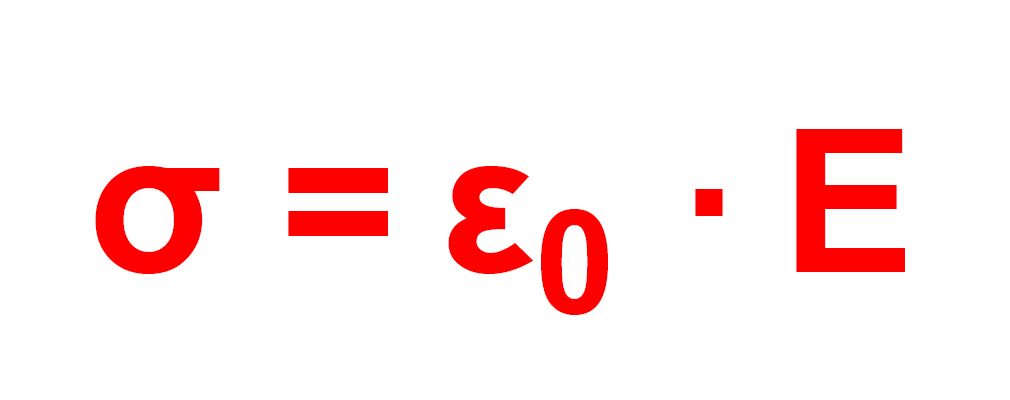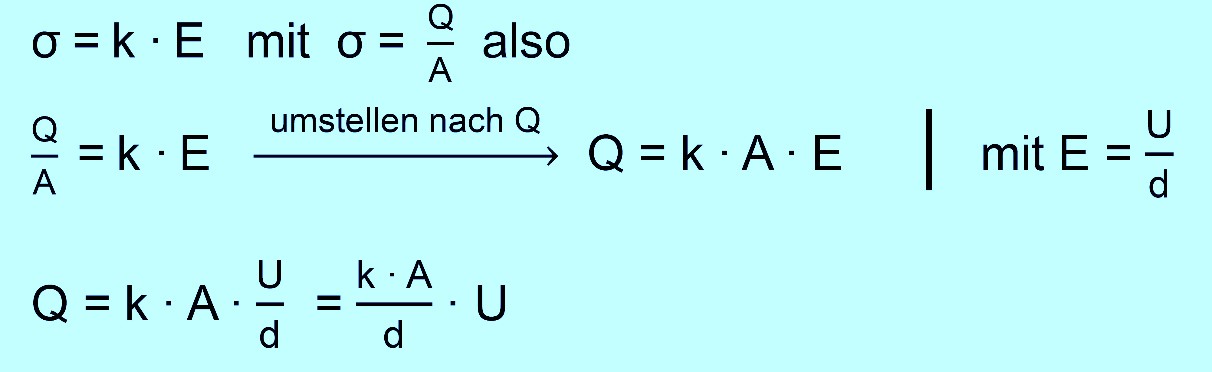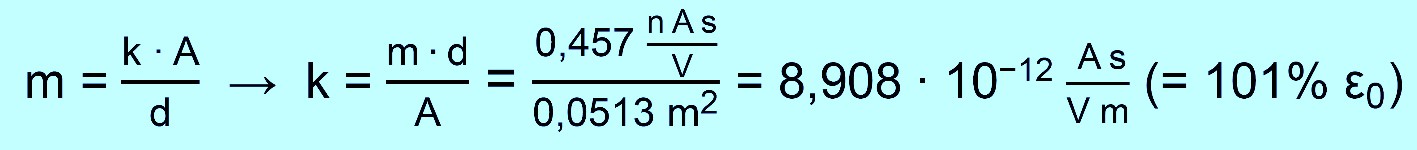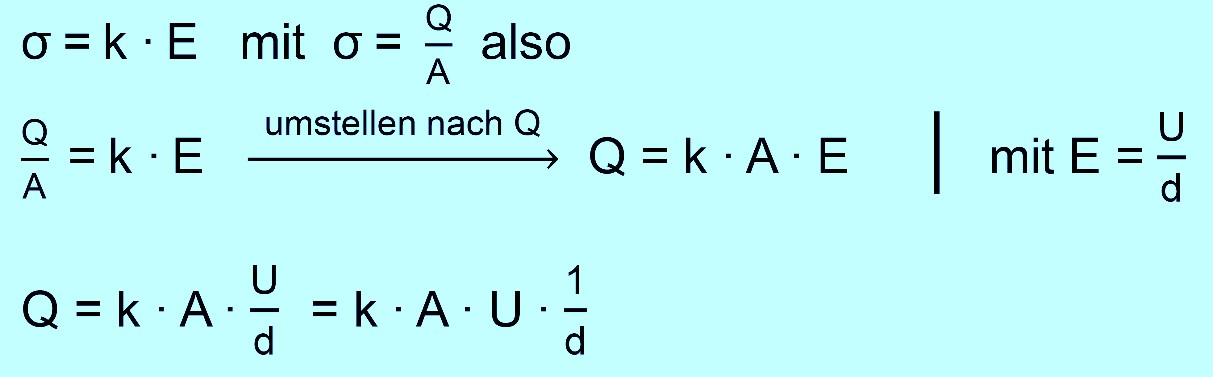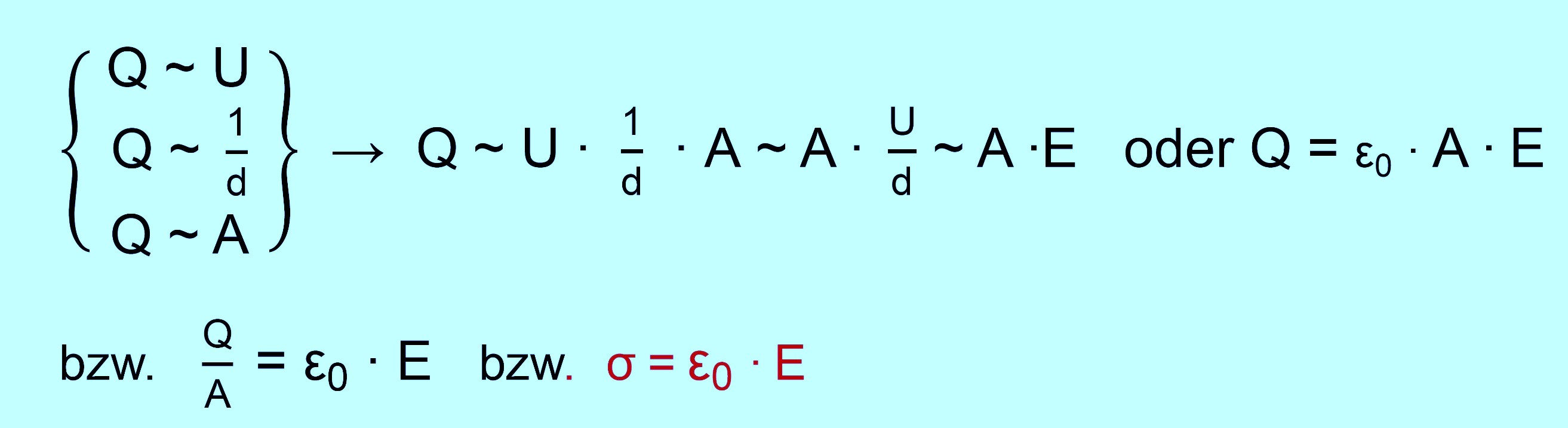|
Flächenladungsdichte-Kondensatorladung Definition.
Flächenladungsdichte Wir wollen uns in diesem Kapitel mit der Ladung auf Platten eines Kondensators beschäftigen. Hierzu definieren wir uns zunächst die Größe „Flächenladungsdichte“ σ. Aus der Definition heraus werden wir den Zusammenhang zur Feldstärke herstellen. Diese Zusammen- hänge werden danach noch experimentell bestätigt. Also zunächst zur Flächenladungsdichte. Wie der Name schon sagt, geht es um die Dichte von Ladungen. Aus der Mechanik würde man denken, es geht darum, wie viele Ladungen pro Volumeneinheit auf einem Körper vorliegen, also ähnlich wie bei der Massendichte (ρ = m/V). Die Ladungen sind aber in einem geladenen Körper nicht gleichmäßig über den Körper verteilt. Gleichnamige Ladungen stoßen sich ja ab. Also werden die Ladungen den größten Abstand vonein- ander einnehmen und sich somit auf der Oberfläche des geladenen Körpers befinden. Hieraus ergibt sich folgende Definition über die Fläche und nicht über das Volumen.
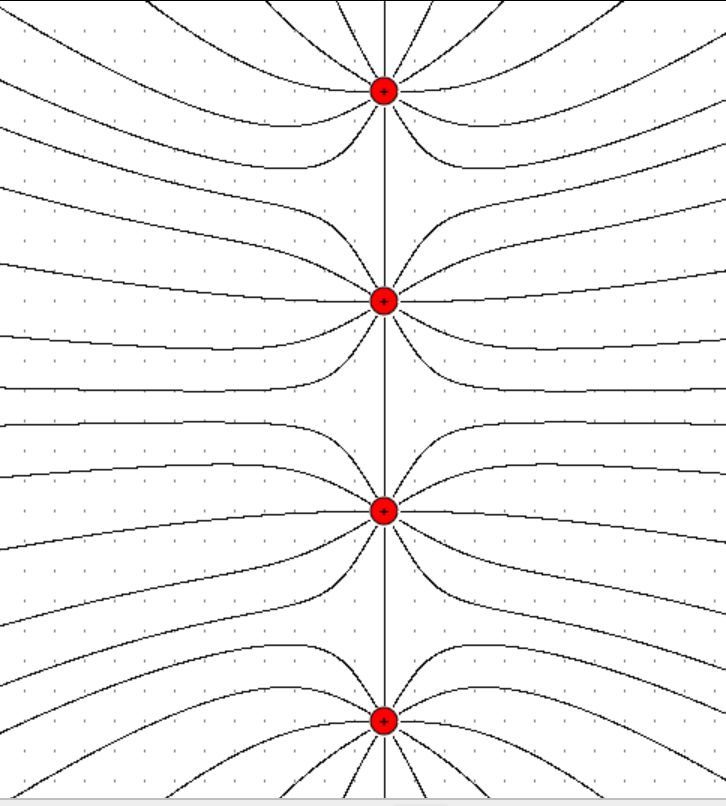
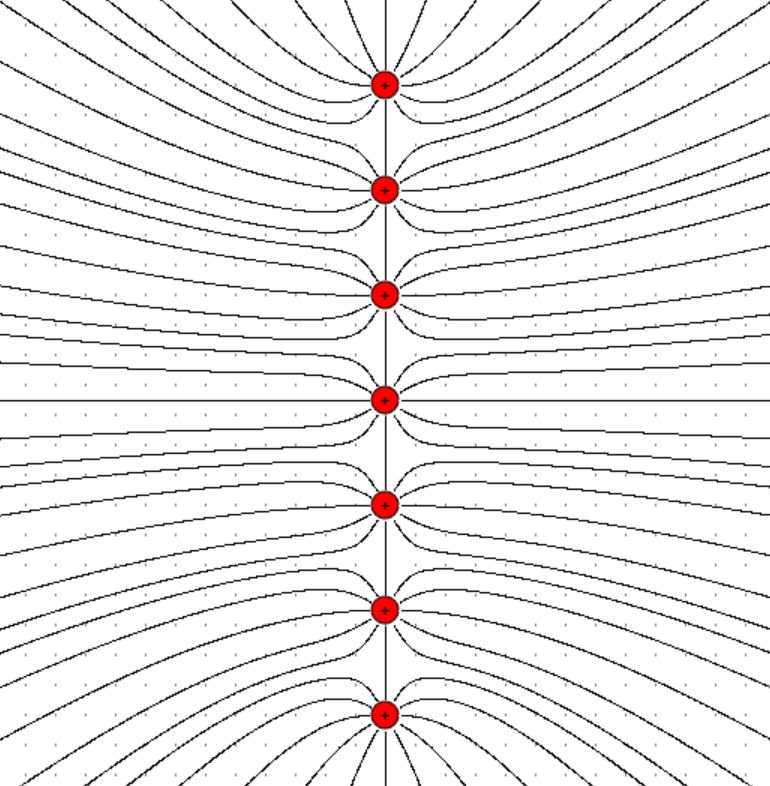
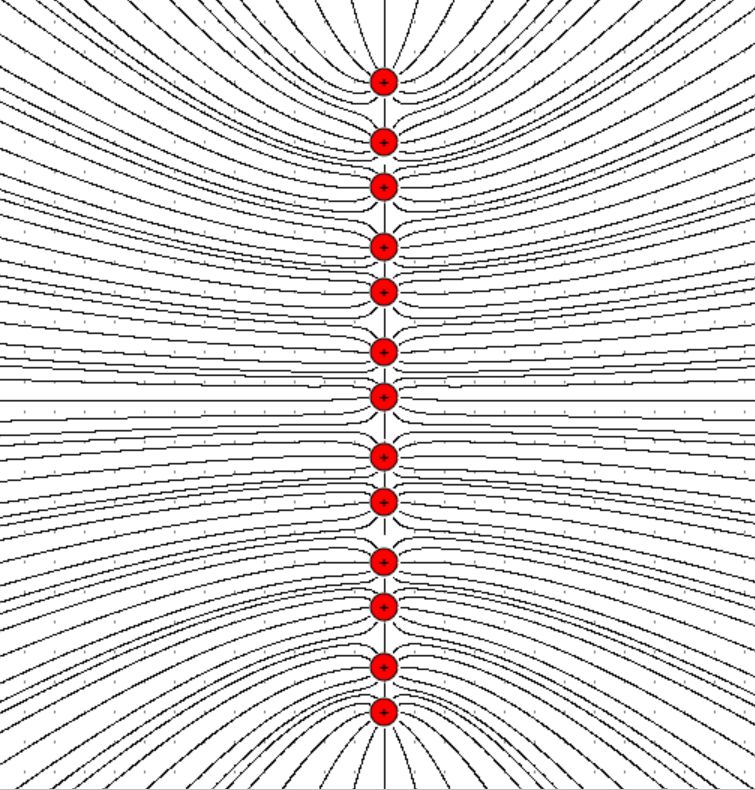
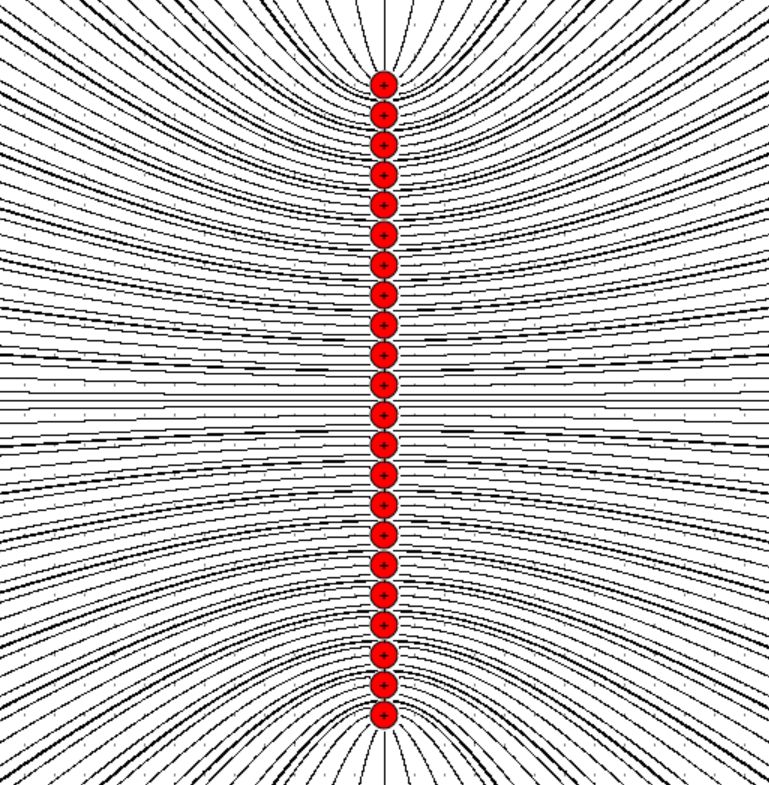
Je mehr Ladungen wir auf einer Flächeneinheit haben, desto mehr elektrische Felder gibt es auch, da jede Ladung ein eigenes elektri- sches Radialfeld erzeugt. Die Summe aller Einzelfelder ergibt das Gesamtfeld. (Hinweis: hiermit errechnet das
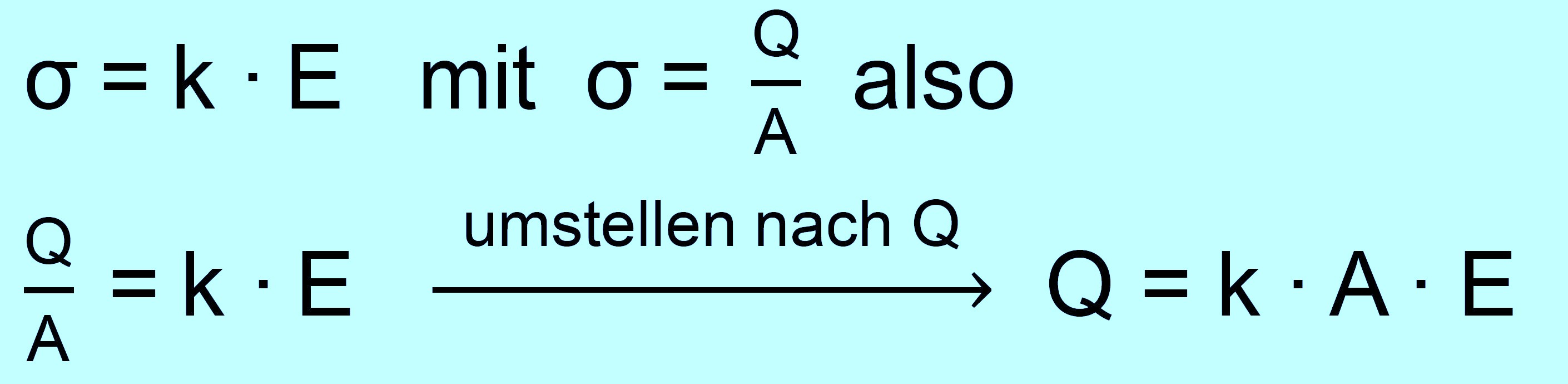
Programm von Prof. Girwidz seine Felder) Die Feldliniendichte muss also immer größer werden, je mehr Einzel- ladungen pro Flächeneinheit vorliegen. Es ist daher folgerichtig einen Zusammenhang zwischen Flächenladungsdichte σ und der elektri- schen Feldstärke E (Feldliniendichte) aufzustellen. Der einfachste Zusammenhang wäre ein proportionaler, also σ = k ∙ E (k = Propor- tionalitätskonstante). Mit dem Programm von H. Girwidz kann man den Zusammenhang auch verständlich machen. Ich habe hierzu einmal verschiedene Feld- linienbilder bei unterschiedlicher Ladungsdichte zeichnen lassen. Hier die Bilder:
Man erkennt schön, dass die Feldliniendichte mit zunehmender Ladungsdichte auch zunimmt. Messungen - Versuchsreihen Prinzipiell kann man bei den Messungen zwei Versuchsreihen unter- scheiden. 1. Messverfahren
mit Elektrofeldmeter Aufbau Man hat ein Elektronenfeldmeter zur Verfügung (s.Elektrische Feld-stärke). In diesem Fall kann man direkt den Zusammenhang zwischen Q und E aufstellen. Man benötigt noch ein Messgerät zur Bestimmung kleiner Ladungsmengen. Hierzu wurde
häufig der Gleichstrommess- verstärker von Phywe (11742.93) benutzt, der z.Z. bei Phywe nicht mehr zur Verfügung steht, aber wohl in vielen Sammlungen noch an- zutreffen ist. Der Aufbau kann dann folgendermaßen aussehen:
Hinweis:
die Versorgungsspannung für das Elektrofeldmeter ist nicht zu sehen und
befindet sich unterhalb der Tischplatte. Erklärung des Aufbaus: Das Elektrofeldmeter ist an den zugehörigen Kondensatorplatten be- festigt. An einem Messgerät wird die Feldstärke E „indirekt“ abgelesen. Die Konduktorkugel 1 wird an das Spannungsnetzgerät angeschlos- sen. Mit diese Kugel berührt man dann die linke Kondensatorplatte und lädt diese dadurch mit einer bestimmten Ladung Q auf. Diese Ladungsmenge kann über die übertragene Spannung geändert wer- den. Die Ladung Q wird über die Konduktorkugel 2 durch Berührung der Platte abgegriffen und an den Gleichstrommessverstärker weiter- geleitet. Über ein Messgerät kann Q registriert werden. Man erhält also „Q“ und „E“ als Messgrößen und kann diese Werte jetzt z.B. mit Excel weiter untersuchen. Messungen Im Folgenden einmal ein paar Messwerte, die von meinem GK im Jahr 2008-09 gemessen wurden.
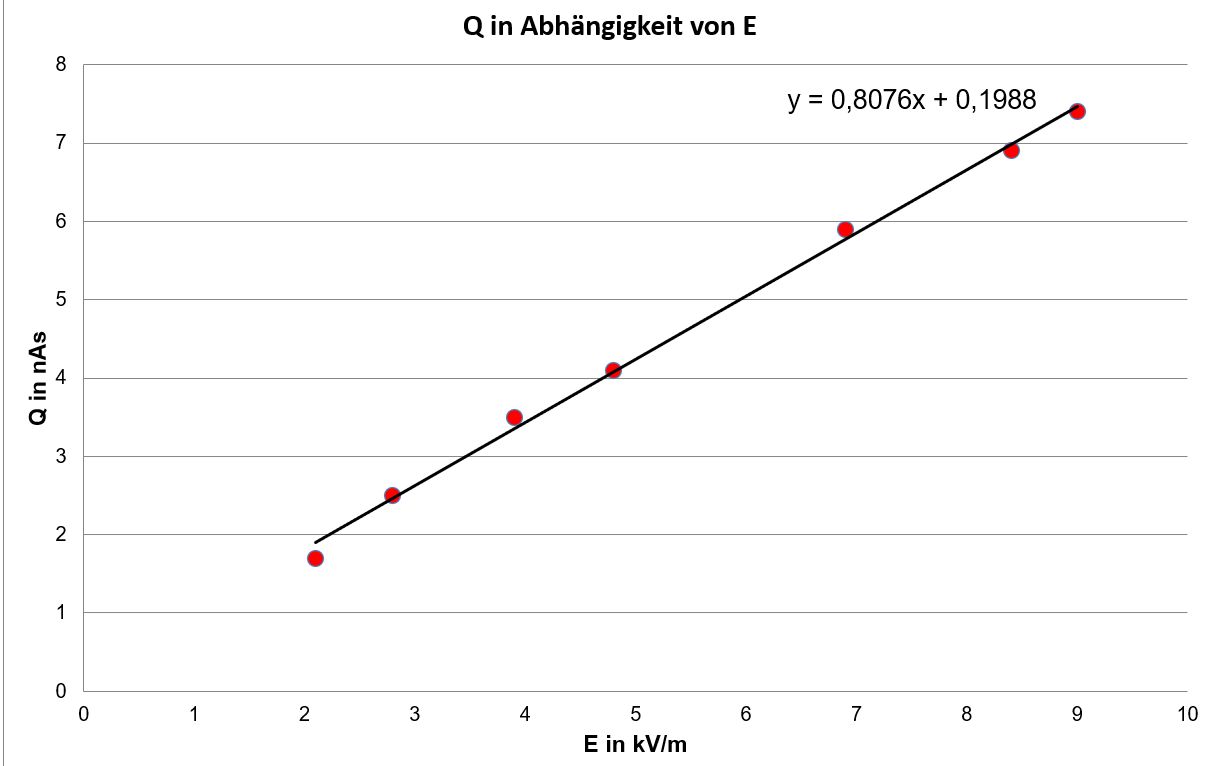
Die Auswertung ergibt das Diagramm
Es ergibt sich ein recht guter linearer Zusammenhang. Hinweis:
Es könnte ein systematischer Fehler vorliegen, weil die Gerade nicht durch
den Ursprung geht, sondern nach
oben verschoben ist. Es ergeben sich aus der Vermutung die folgenden Gleichungen:
Es müsste also nach der Vermutung ein linearer Zusammenhang vorliegen. Dies wurde durch die Messungen bestätigt. Die Steigung „m“ der Trendlinie entspricht also „ k
∙ A “. Mit A = 0,08 m2 ergibt sich für k aus diesen Messungen:
Die Konstante „k“ wird elektrische Feldkonstante genannt und mit ε0 abgekürzt. In Formelsammlungen findet man für ε0 = 8,854 ∙ 10−12 As/Vm. Wir liegen mit den Messungen (114%) also etwas daneben. Zusammenfassend ergibt sich jetzt also:
Hinweis:
Wir haben zur Herleitung die Umstellung Q = ε0 ∙ A ∙
E benutzt. Ein aufmerksamer Leser
wird bemerken, dass wir zur Bestätigung der Gleichung eigentlich auch noch
zeigen müssten,
dass Q proportional zu A ist. Leider lässt sich dies aufgrund der mangelnden Zahl an
Plattenkondensatoren unterschiedlicher Fläche nicht messtechnisch zeigen und
wird als selbstverständlich vorausgesetzt. 2. Messverfahren ohne Elektrofeldmeter Wenn man kein Elektrofeldmeter hat, muss man mindestens ein Ladungsmessgerät aufweisen, um überhaupt Messungen durchführen zu können. Es sollte also mindestens so etwas ähnliches wie der Gleichstrommessverstärker von Phywe vorliegen. Aufbau Zunächst wieder ein Bild von einem möglichen Versuchsaufbau.
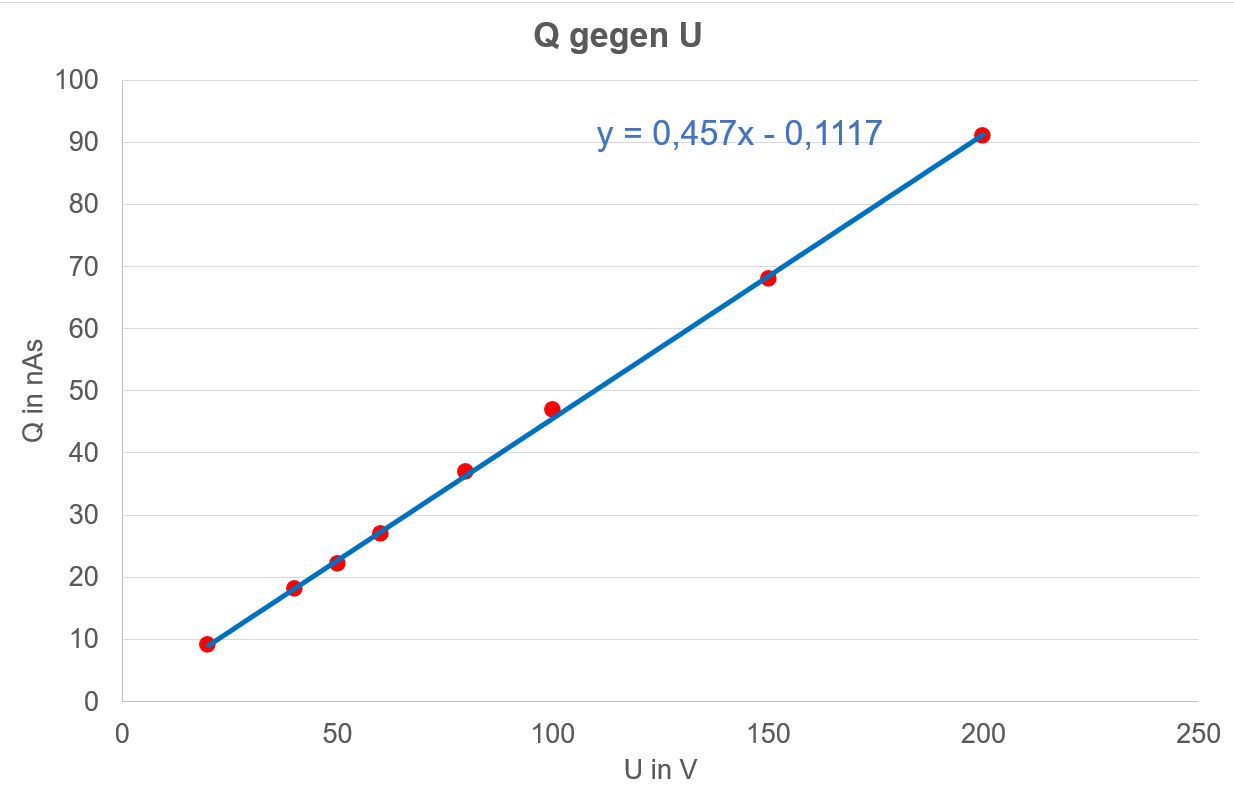
Der Aufbau enthält viele Bestandteile des ersten Versuchsaufbaus. Wir finden wieder die Konduktorkugeln zur Übertragung der Span- nung (1) bzw. Abnahme der Ladung (2). Die rechte isolierte Platte wird benutzt. Die linke Platte ist geerdet. Auf der rechten Platte hat es sich bewährt einen Metallstift einzufügen, um besser auf die Innenseite des Kondensators zu gelangen. Netzgerät und Voltmeter, Gleichstrom- messverstärker und Anzeigegerät sind geblieben. Es kann ein anderer Plattenkondensator benutzt werden, bei dem die Abstände besser ein- stellen werden können. Da „E“ nicht direkt gemessen wird, muss man zwei Messungen vor- nehmen, nämlich die Abhängigkeit der Ladung „Q“ von „U“ und „d“. Es liegt ja die Formel E = U/d als Grundlage vor. Zur Abhängigkeit von A gilt der Hinweis von oben am Ende des 1. Messverfahrens. Messungen 1. Messung: Q gegen U, d=konstant, A=konstant Im Folgenden einmal ein paar Messwerte, die von mir selbst aufge- nommen wurden ( d = 1 mm, A = 0,0513 m2).
Die Auswertung als Excel-Diagramm ergibt:
Es ergibt sich ein sehr guter linearer Zusammenhang. Da praktisch eine Ursprungsgerade vorliegt, ergibt sich sogar die Proportionalität, was mit den Gleichungen im Einklang wäre.
Es müsste also nach den Gleichungen eine Proportionalität vorliegen. Was mit den Messungen eindeutig bestätigt wird. Für ε0 ergibt sich ein ungewöhnlich genauer Wert aus den Messungen.
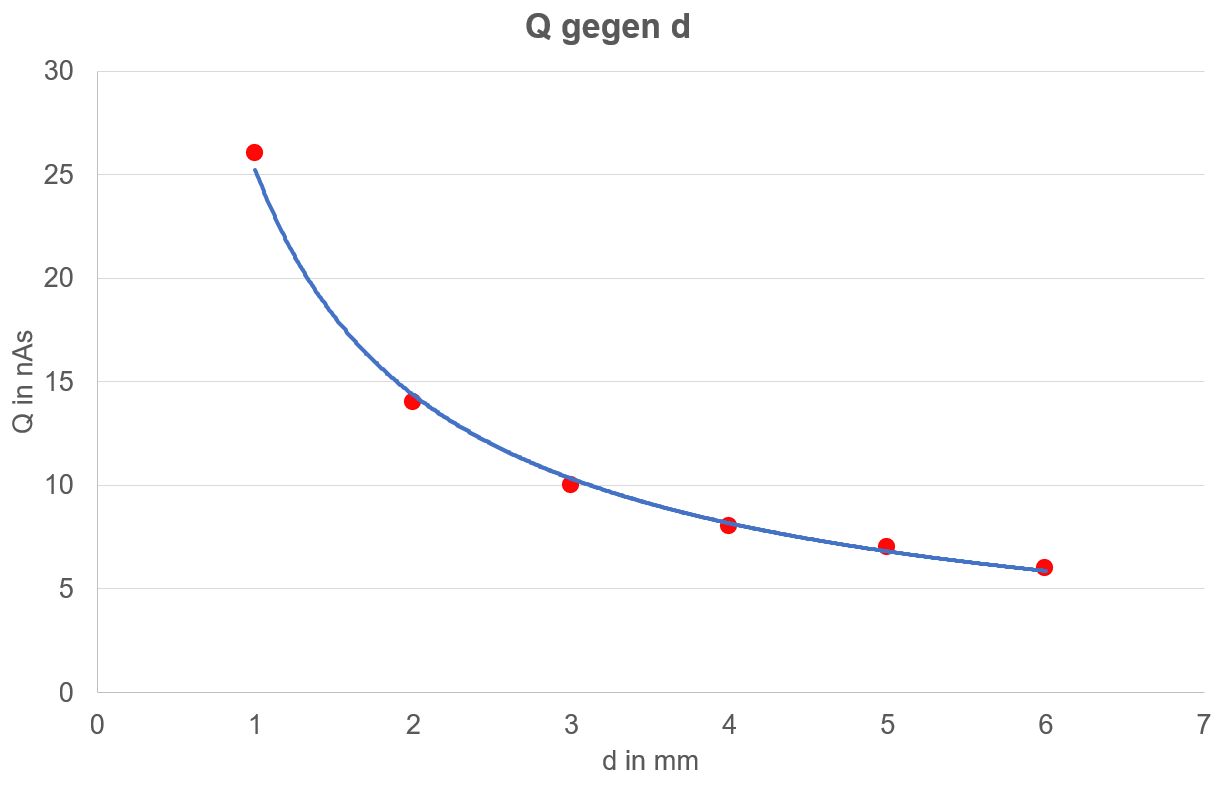
Um die Vermutung vollständig zu bestätigen, muss noch die Abhängig- keit zwischen Q und d untersucht werden. 2. Messung: Q gegen d, U=konstant, A=konstant Messung aufgenommen vom GK 98/99 mit U=60 V, A=0,0513 m2
Diagramm:
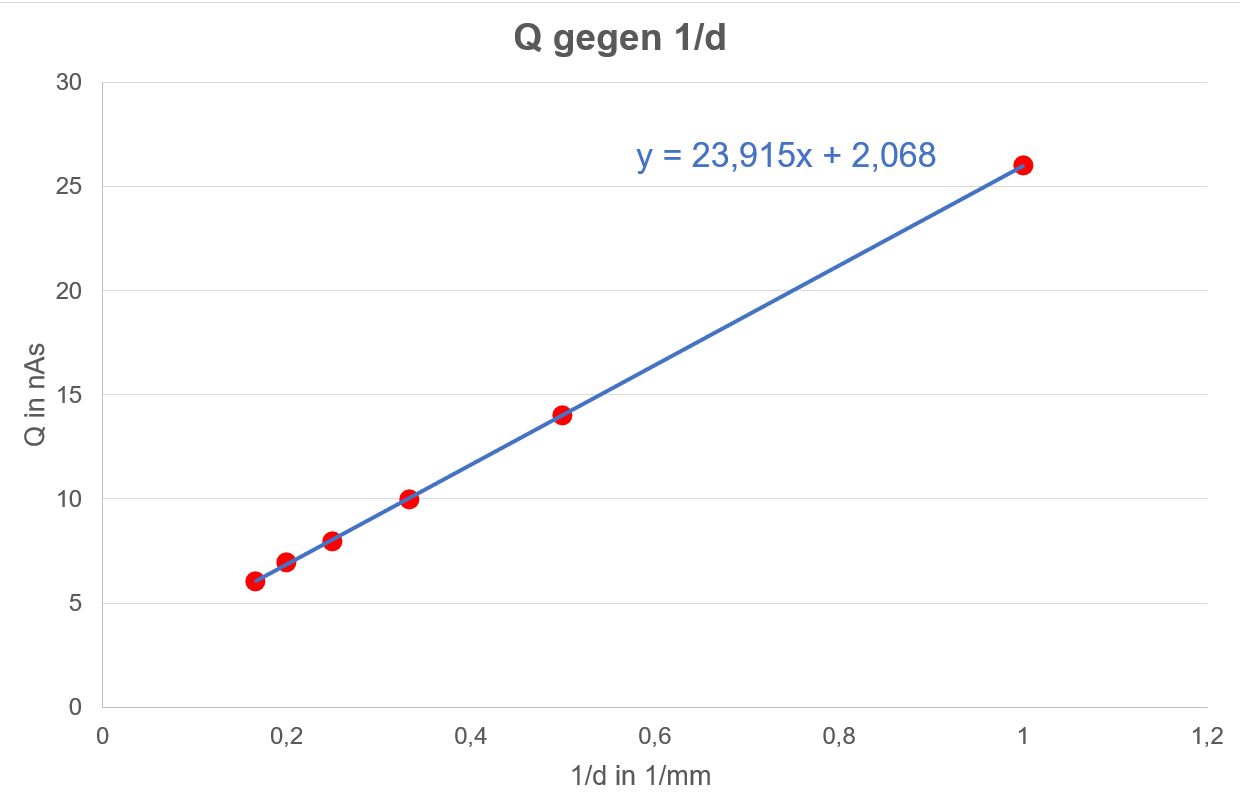
Es könnte eine Hyperbel vorliegen. Um dies zu bestätigen, wird Q gegen 1/d aufgetragen.
Diagramm:
Gleichungen hierzu:
Die Proportionalität von Q zu 1/d wird also durch die Messungen be- stätigt. Die Werte für ε0 sind leider nicht so gut wie bei der ersten Messung.
Zusammenfassung Unsere
Vermutung, dass σ = k ∙ E gilt, wird durch alle Messungen be- stätigt. Alternative: aus der Messung zur
Formel Wir sind in diesem Kapitel etwas ungewöhnlich vorgegangen, weil wir von einer Vermutung ausgingen und diese bestätigten. Man kann natürlich auch einfach die Messergebnisse nehmen und daraus die den Zusammenhang aufstellen. Dies sähe dann folgendermaßen aus.
Wer das Ganze noch einmal aus einer anderen Perspektive sehen möchte, kann sich folgendes Video von Benno Köhler ansehen, der auch die entsprechenden Messungen mit einem anderen Aufbau (Leybold-Geräte) durchführt. Hinweis:
- mir
kommen die Messungen etwas umständlich vor, weil er Geräte trennen muss und ver- schiedene
Schalter benutzt. Die Benutzung der Konduktorkugel
hat sich meiner Meinung nach bewährt. - das
aufgeführte Video ist geschnitten und neu zusammengesetzt. Wer das Video
vollständig ansieht,
wird merken, dass H. Köhler andere Formeln aus den Messungen ableitet. Wir
werden diese Formel aus dem in diesem Kapitel gewonnenen Zusammenhang
zwischen σ
und Q noch herleiten. Video Benno Köhler (geschnitten und neu zusammengesetzt) Quelle: Physik LK 5 -
Kondensator Teil 1 - YouTube zu
Abschnitt: - Def. Flächenladungsdichte - Vermutung - 1
Versuchsreihe-Aufbau - 1.Versuchsreihe-Messungen+Auswertung - 2.
Versuchsreihe-Aufbau - 2. Versuchsreihe-Messungen+Auswertung
Q gegen U - 2. Versuchsreihe-Messungen+Auswertung
Q gegen d - Zusammenhang zwischen σ und E - Kapitel
„Plattenkondensator“ |