|
Versuchsaufbau Bevor wir uns genauer mit dem Begriff „Dielektrikum“ beschäftigen, schauen wir zunächst auf die Ergebnisse eines einfachen Versuches. Der Versuchsaufbau ist praktisch
derselbe wie im Versuch
zur Kon- densatorladung. Man gibt jetzt nur zwischen die Platten ein isolieren- des Material, eben das Dielektrikum. In diesem Fall wird eine Glas- platte genommen und man misst wieder die aufgeflossene Ladungs- menge. Hier noch einmal der alte Versuchsaufbau
Man schiebt jetzt nur bei der ersten Messung eine
Glasscheibe zwischen die Platten. Das sieht dann in etwa wie in dieser Abbildung aus.
Danach nimmt man die Glasscheibe heraus, so dass der Abstand d beibehalten wird. In beiden Fällen wird die aufgeflossene Ladungs- menge Q bei gleicher Spannung gemessen. Der Unterschied zwischen den Versuchsaufbauten besteht also nur darin, dass sich bei der ersten Messung eine Glasscheibe zwischen den Kondensatorplatten befindet. In beiden Messungen sind d, A und U konstant. Messergebnisse: U = 100 V, d konstant = Dicke der Glasscheibe, A konstant = 0,0513 m2 mit Glasscheibe: Q = 88 nAs ohne Glasscheibe: Q = 16 nAs Man erkennt, dass bei dem Versuch mit Glasscheibe deutlich mehr Ladungen bei gleicher Spannung
gespeichert werden können. Die Kapazität C = Q/U hat also zugenommen. Dies wird zur Erhöhung der Kapazität bei der technischen Anwendung von Kondensatoren (Kapitel dazu in Arbeit) benutzt.
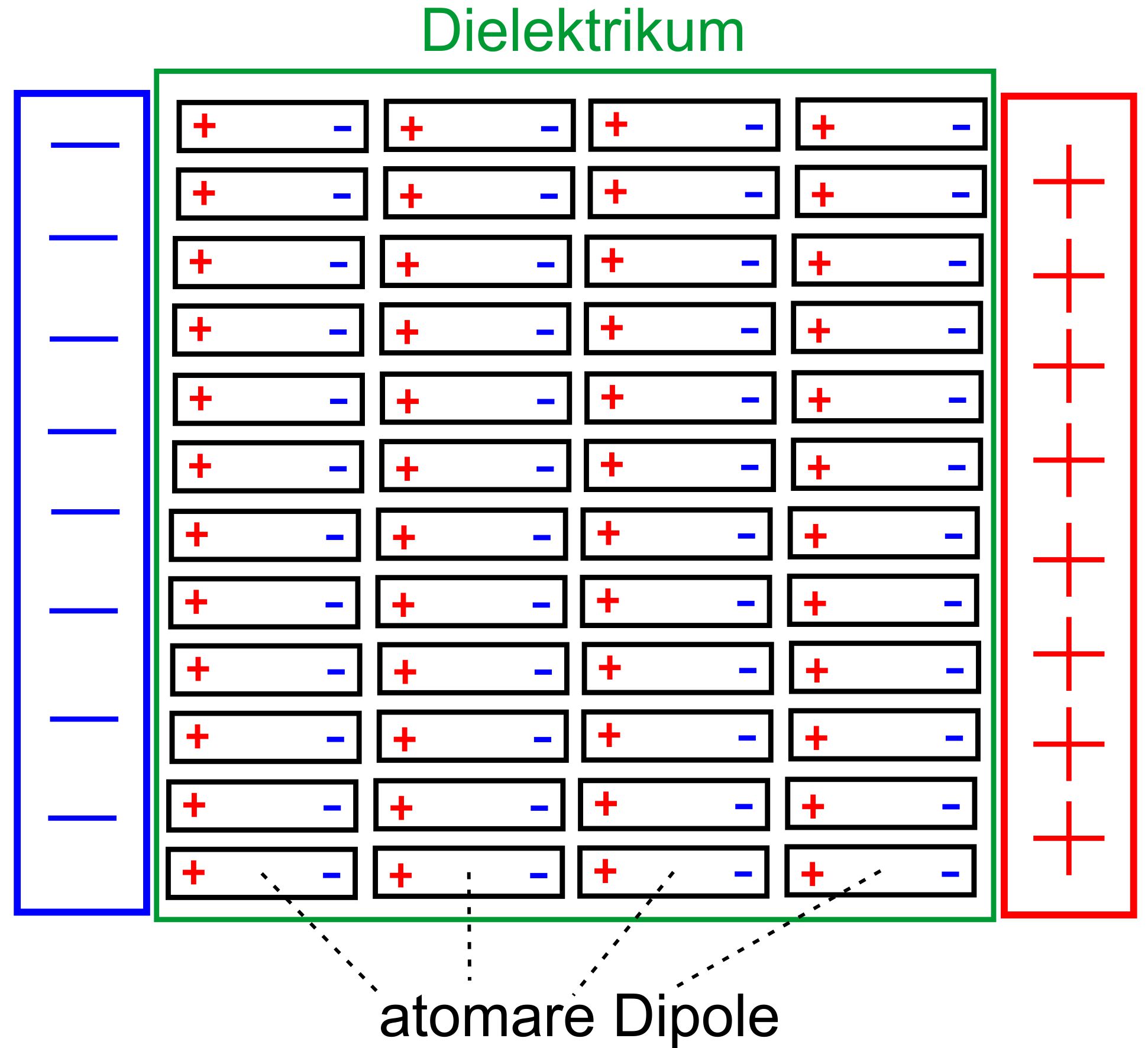
Erklärung der Kapazitätserhöhung Allgemeine Bemerkungen In einem Nichtleiter gibt es keine freien Elektronen. Durch ein äußeres elektrisches Feld können die Ladungen nur innerhalb des Atoms ver- schoben werden. Die Atome werden zu Dipolen. Es liegen ähnliche Bedingungen wie im Kapitel „Elektrische Feldstärke“ beim Nachweis des elektrisches Feldverlaufes vor. Die Verhältnisse im Kondensator mit Dielektrikum sehen also in etwa wie folgt aus.
1. Fall: U bleibt konstant Wenn die
Kapazität zunimmt, muss Q zunehmen, wenn U konstant ist. Es gilt
ja C = Q/U. Die
Erklärung ist recht einfach. Die atomaren Dipole haben sich ja durch
Influenz im elektrischen Feld ausgerichtet. Es sind Oberflächen- ladungen
entstanden, die den Ladungen des Kondensators gegen- überstehen.
Dadurch wird ein Teil der Kondensatorladungen gebun- den. Man
könnte auch salopp sagen: „die Ladungen neutralisieren sich“.
Dadurch kann die äußere Spannung wieder weitere Ladungen auf die
Kondensatorplatten aufbringen. Die Anzahl der Ladungen auf den
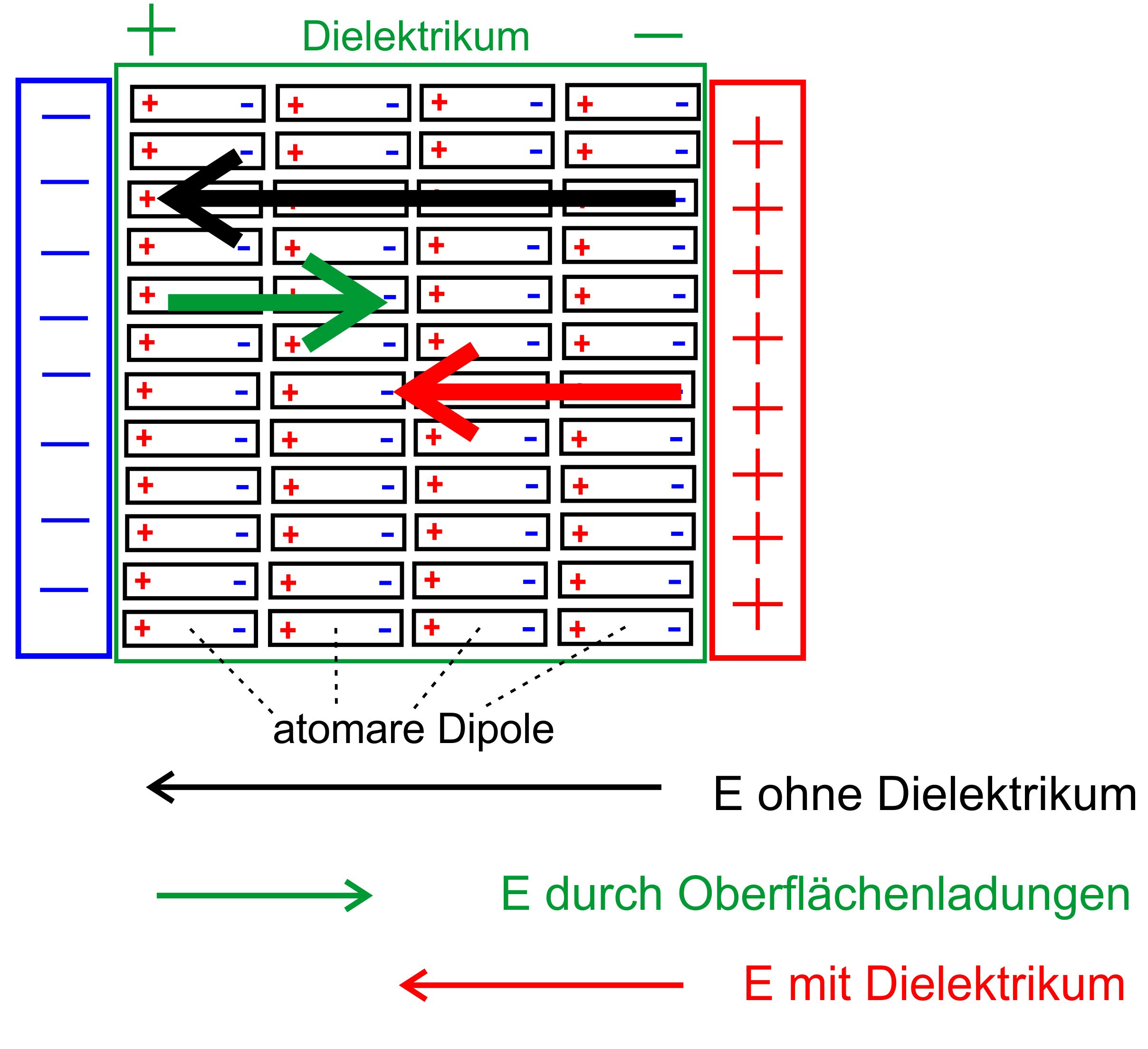
Kondensatorplatten hat sich erhöht. 2. Fall: Q bleibt konstant Jetzt muss U abnehmen. Durch die Oberflächenladungen entsteht ein Gegenfeld zum äußeren elektrischen Feld. Das resultierende Gesamtfeld ist schwächer als das elektrische Feld ohne Dielektrikum. Mit U = E ∙ d ergibt sich also eine geringere resultierende Spannung. Die Kapazität hat sich erhöht. Die Situation sieht folgendermaßen aus.
Dielektrizitätskonstante
(Permittivität) Die Vergrößerung der Kapazität durch ein Dielektrikum wird durch die Dielektrizitätskonstante oder relative Permittivität gekennzeichnet. Sie hängt natürlich vom Material ab, welches als Dielektrikum benutzt wird. Diese Zahl wird mit εr gekennzeichnet. εr gibt an, um welchen Faktor die Kapazität erhöht wurde. Es gilt also:
Man erhält somit für die Bestimmung der Kapazität mit Dielektrikum folgende Formel.
Hinweis:
Diese Formel ist nur korrekt, wenn das Dielektrikum den Kondensator
vollständig ausfüllt.
Für den Fall, dass das Dielektrikum dünner als der Abstand der Kondensatorplatten
ist, schaue man sich die Übungsaufgabe Nr.3 an.
Werte für εr findet man bei wikipedia oder in folgender PDF. Für die
Glasscheibe aus unserem obigen Versuch ergibt sich εr
= 880 pF/160 pF = 5,5 Linkliste
zum Thema:
zu
Abschnitt: - Versuch
- Def.
Dielektrikum - Erklärung der Kapazitätserhöhung - Def.
Dielektriziätskonstante - Kapitel
„Plattenkondensator“ |