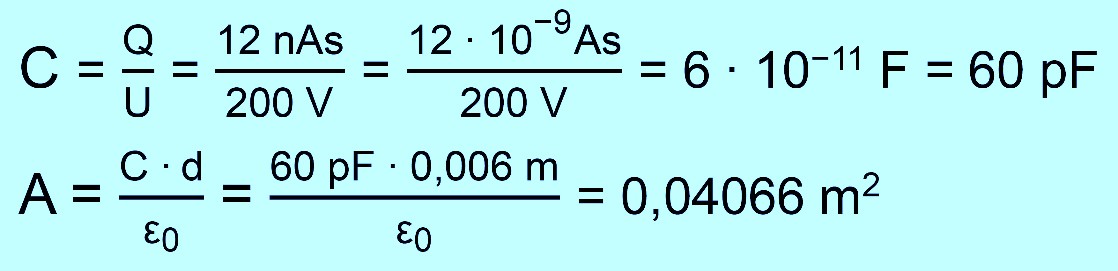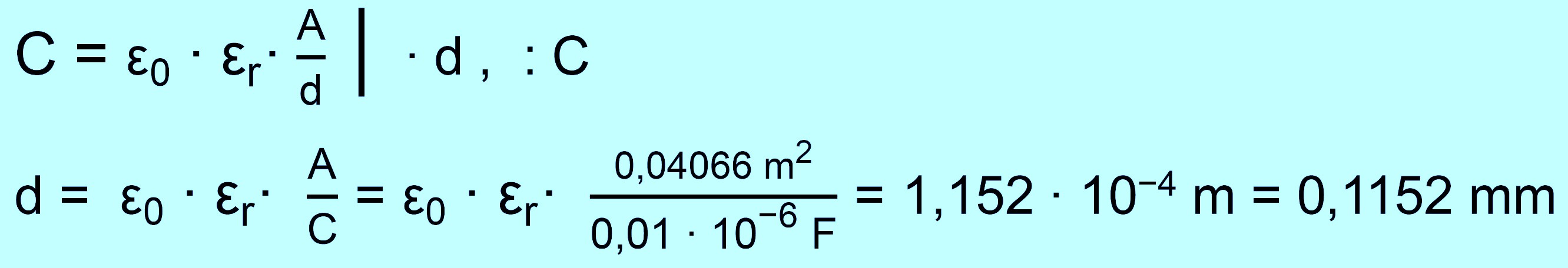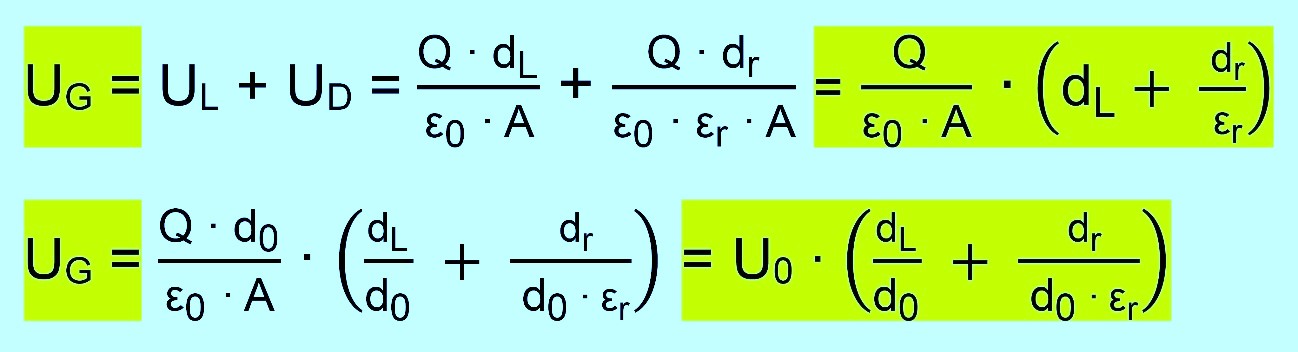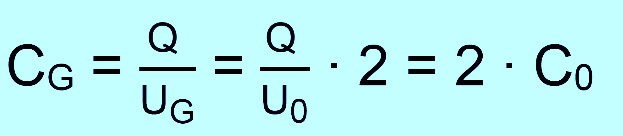Übungsaufgaben-Dielektrikum

Aufgabe Nr.1 (einfach)

Es liegt ein Plattenkondensator mit kreisförmigen Platten vor. Der Durchmesser der Platten beträgt 25 cm.

a.) Die Platten haben zunächst einen Abstand von 5 cm. Zwischen den

Platten befindet sich Luft.

b.) Jetzt wird eine 9 mm dicke Glasplatte ( ε_r = 7 ) eingeschoben und

die Platten werden an die Glasplatte gedrückt. Die Glasplatte füllt

somit den gesamten Raum zwischen den Platten aus.

Bestimme jeweils die Kapazität. Gib die aufgeflossene Ladungs-

menge an, wenn bei a.) eine Spannung von 100 V und bei b.) 10kV angelegt wird.

Hinweis: Bei einem Kondensator mit Dielektrikum kann man höhere Spannungen anlegen als

bei einem Luftkondensator, da das Dielektrikum die Durchschlagfestigkeit deutlich erhöht.

(Link zur Durchschlagfestigkeit-wikipedia)

Lösung:

zu a.) wir benutzen die bekannten Formeln für C und Q

zu b.) es wird die Kapazitätsformel mit Dielektrikum benutzt

Aufgabe Nr.2 (einfach, mittel)

a.) Ein Plattenkondensator weist bei einer Spannung von 200 V eine

gespeicherte Ladungsmenge von Q = 12 nAs auf. Berechne die

Kapazität des Kondensators und die Plattenfläche, wenn d = 6 mm

beträgt.

b.) Man gibt jetzt einen Paraffinbogen ( ε_r = 3,2 ) zwischen die Platten,

so dass der Kondensator vollständig ausgefüllt ist. Die Kapazität soll

dabei auf 0,01 µF gesteigert werden. Wie dick darf dann der Bogen

nur sein?

Lösung:

zu a.)

zu b.)

Aufgabe Nr.3 (schwer)

In der folgenden Aufgabe füllt das Dielektrikum den Kondensator

nicht vollständig aus. In diesem Fall kann nicht so einfach wie bisher

gerechnet werden.

Ein Kondensator weist einen Abstand der Platten von 8 mm auf. Man

gibt jetzt ein Dielektrikum hinein, das die gleiche Fläche wie die Kon-

densatorplatten aufweist, aber nur 6 mm dick ist. Man lädt den Kon-

densator zunächst ohne Dielektrikum mit der Spannung U₀ auf. Da-

nach klemmt man die Spannungsquelle ab und schiebt das Dielektri-

kum hinein ( ε_r = 3 ). Welche Kapazität liegt jetzt vor? Vergleiche mit dem Kondensator ohne Dielektrikum.

Lösung:

Wo das Dielektrikum genau liegt, ist eigentlich egal. Man kann das

Dielektrikum auch an einer Platte anliegen lassen. Dann hat man

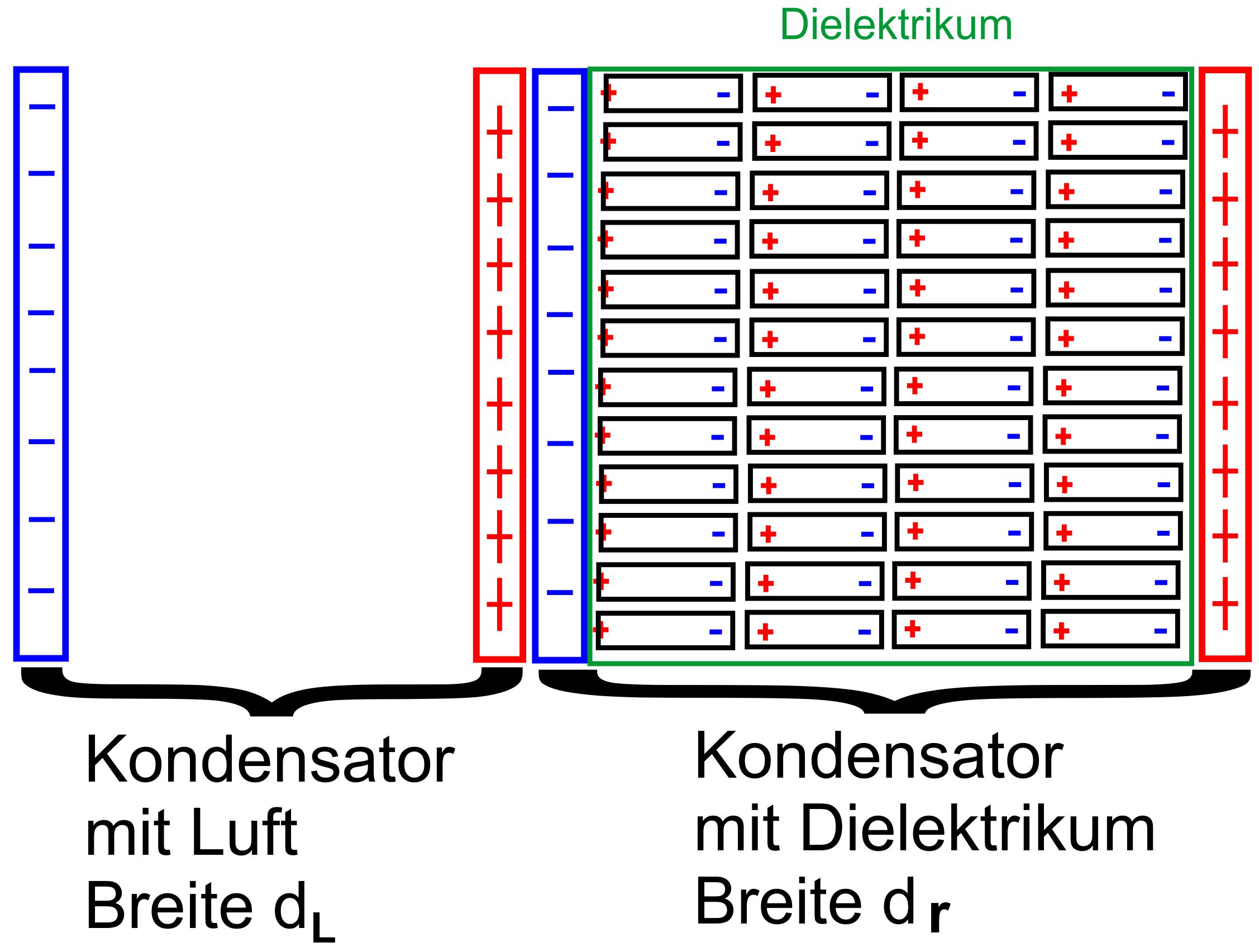
einen Bereich mit Luft und den anderen Bereich mit dem Dielektrikum.

Dies kann man sich als eine Reihenschaltung von Kondensatoren vor-

stellen. Ein Kondensator mit Luft ist in Reihe geschaltet mit einem

Kondensator mit Dielektrikum. (s. Schaltung von Kondensatoren (in Arbeit))

Bei einer Reihenschaltung ist auf beiden Kondensatoren die gleiche

Ladung und die Gesamtspannung U_G ergibt sich durch Addition der

Einzelspannungen U_G = U_L + U_D ( U_L = Spannung am Kondensator mit Luft,

U_D = Spannung am Kondensator mit Dielektrikum)

Die Abbildung zeigt einmal die Verhältnisse.

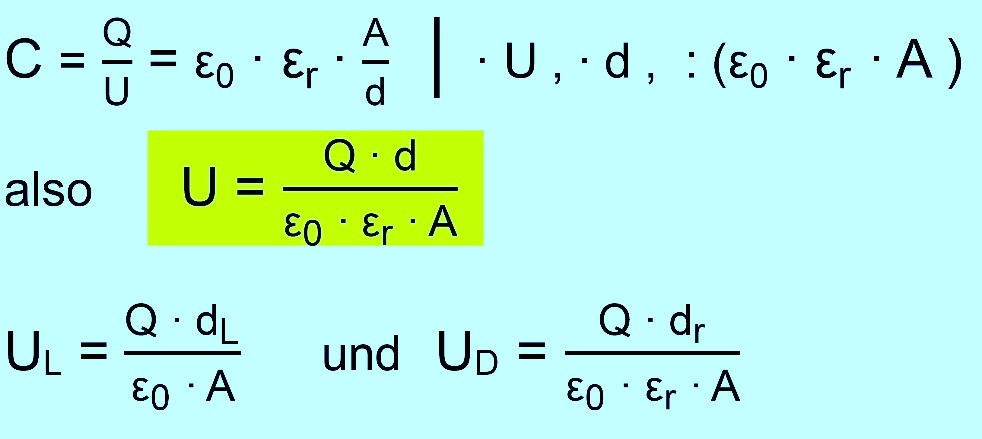
Wir stellen zunächst eine allgemeine Formel für U auf und setzen

dann für die gesuchten Spannungen ein. Es ergibt sich dann:

Wie oben schon bemerkt. ergibt sich die Gesamtspannung aus der

Addition der Einzelspannungen. Q ist konstant. Also gilt:

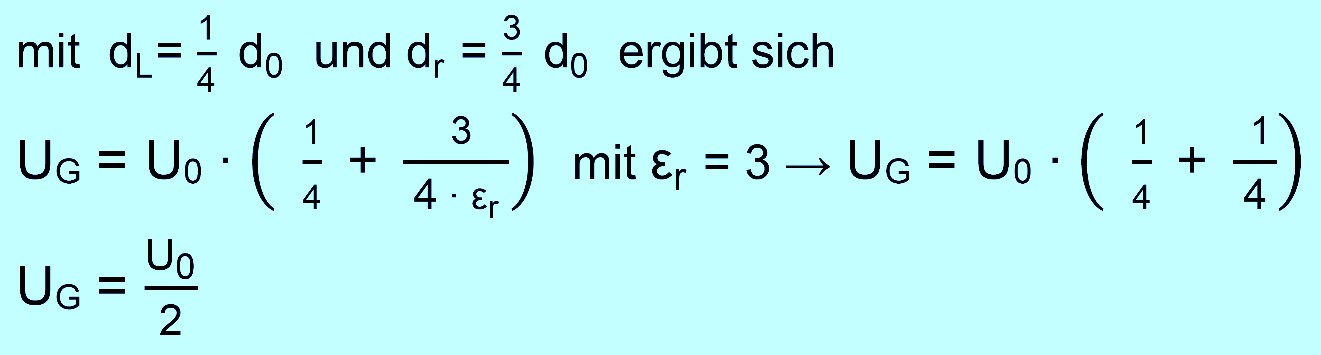
Dies ist eine allgemeine Formel. Man setzt jetzt konkret ein und er-

hält dann die Gesamtspannung.

Also berechnet sich die Kapazität mit der bekannten Formel

Die Kapazität hat sich also verdoppelt.

Hinweis: In der üblichen Fachliteratur (Tipler, Giancoli) wird häufig über die Feldstärke argu-

mentiert. Wer diesen Weg kennenlernen will, sollte dort nachsehen.

- zu Aufgabe Nr.1 - zu Aufgabe Nr.2 - zu Aufgabe Nr.3

- zum Kapitel „Kapazität mit Dielektikum

- zum Kapitel „Kapazität" allgemein

- zum Kapitel „Plattenkondensator“

- zur Übersicht „Felder“