|
Das Elektrische
Feld - Existenz - Feldstärke Existenz eines
elektrischen Feldes Das
elektrische Feld ist an die Eigenschaft „Ladung“ gebunden. Ein Körper,
der geladen ist, soll ein elektrisches Feld aufweisen. Man muss
jetzt also zeigen, dass in der Umgebung eines geladenen Körpers
geladene Probekörper Kräfte erfahren. Versuchsablauf: (leider nur als Text, ich habe kein passendes Video
gefunden bzw. selber aufgenommen; wer ein Video parat hat, soll bitte Kontakt mit mir aufnehmen) Man
lädt eine große Metallkugel (Konduktorkugel) auf
und hält in die Nähe
eine deutlich kleinere geladene Alukugel
(Probekörper). Die Alukugel
kann bifilar (also an zwei Fäden) aufgehängt sein. Man erkennt bei
gleicher Ladungsart, dass die Alukugel dann
abgestoßen wird, d.h.
der Faden wird ausgelenkt, ähnlich wie bei einem Fadenpendel. Die Auslenkung hängt von
der Größe der Ladung der Konduktor- kugel
ab. Außerdem spielt der Abstand der Kugeln und auch die Ladung
des Probekörpers eine Rolle für die
Größe der Auslenkung. Die
Ablenkung geschieht, weil eine Kraft auf die Alukugel
ausgeübt wird.
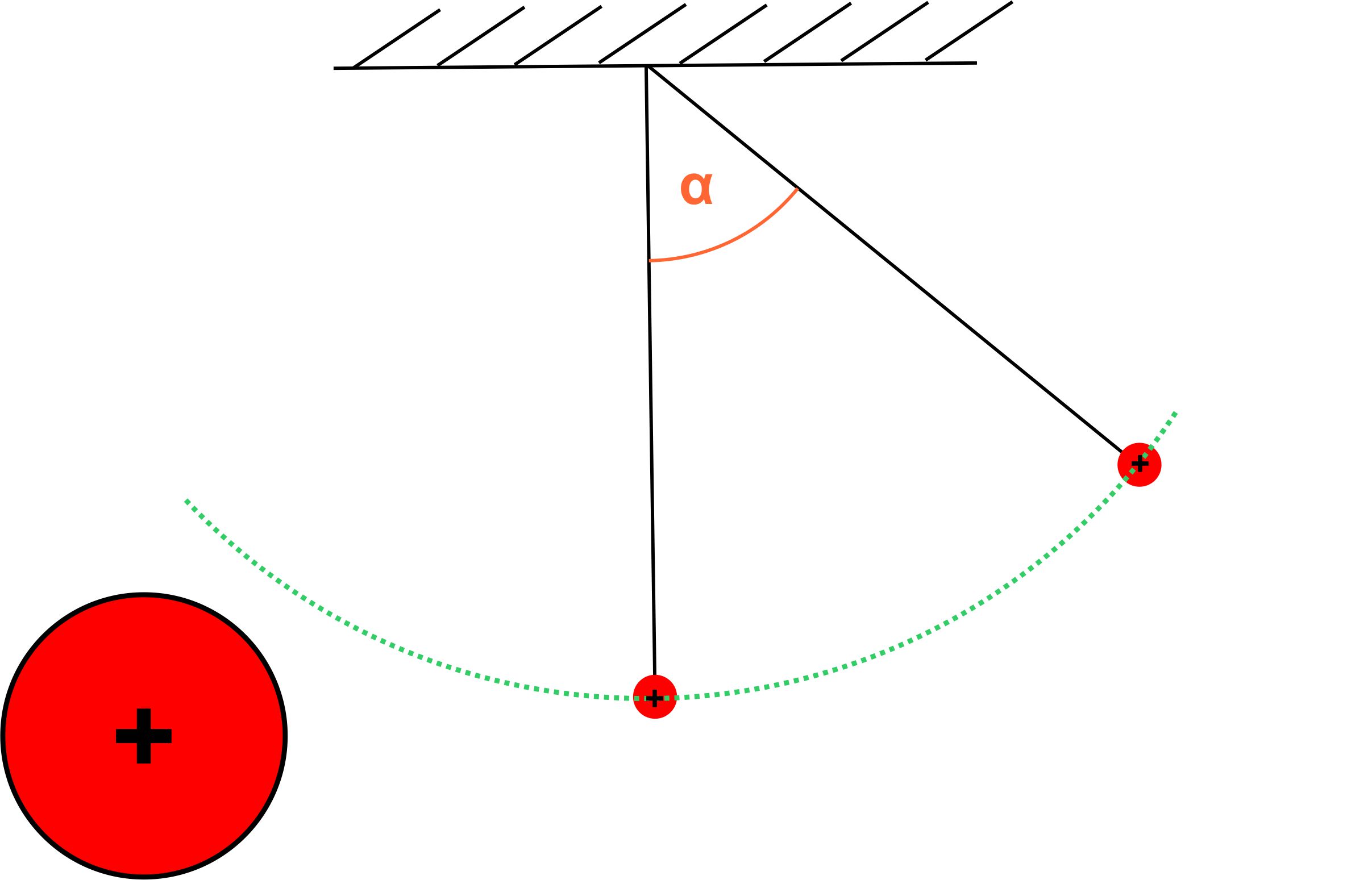
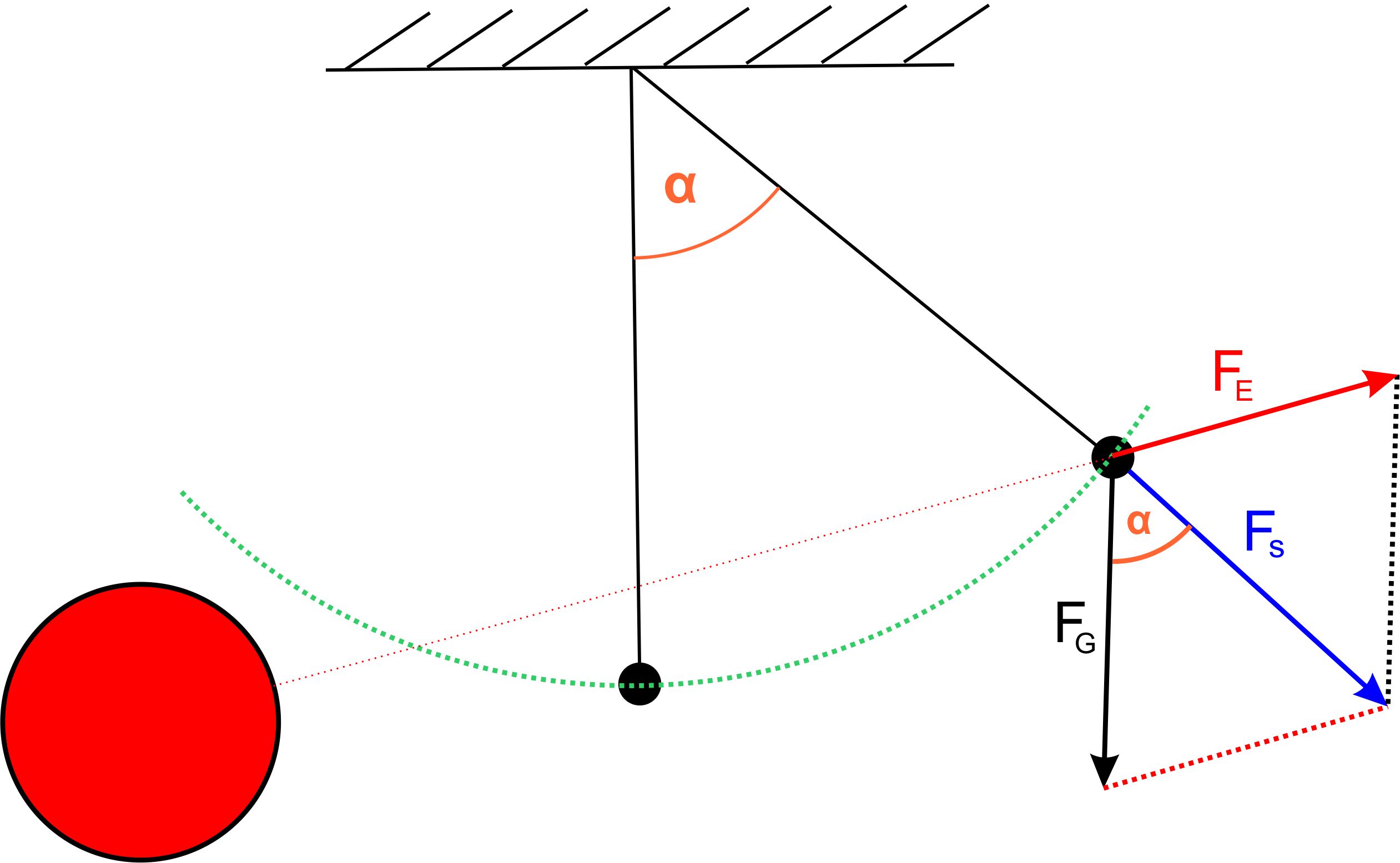
Ein Maß für die Kraft ist der Auslenkungswinkel des Faden- pendels. Hierzu
jetzt zwei Abbildungen:
Wir
halten fest:
Elektrische Feldstärke Für Felder werden im Allgemeinen „Feldstärken“ festgelegt. Die Feld- stärke soll eine Auskunft über die Stärke des Feldes geben, wie ja der Name schon sagt. Was könnte man nun als Feldstärke definieren? Man kommt schnell auf die Kräfte, die auf die Probeladung wirken, also Feldstärke = Kraft auf die Probeladung?? Je größer die Kraft, um so größer die Feldstärke. Wenn man so definieren würde, vergisst man, dass ja die Kraft auf den Probekörper auch von der Ladung des Probekörpers abhängt. Deswegen muss man diese Eigenschaft her- ausdividieren oder anders formuliert, die Kraft auf eine Einheitsladung von 1 C wählen. Es ergibt sich somit als Definition:
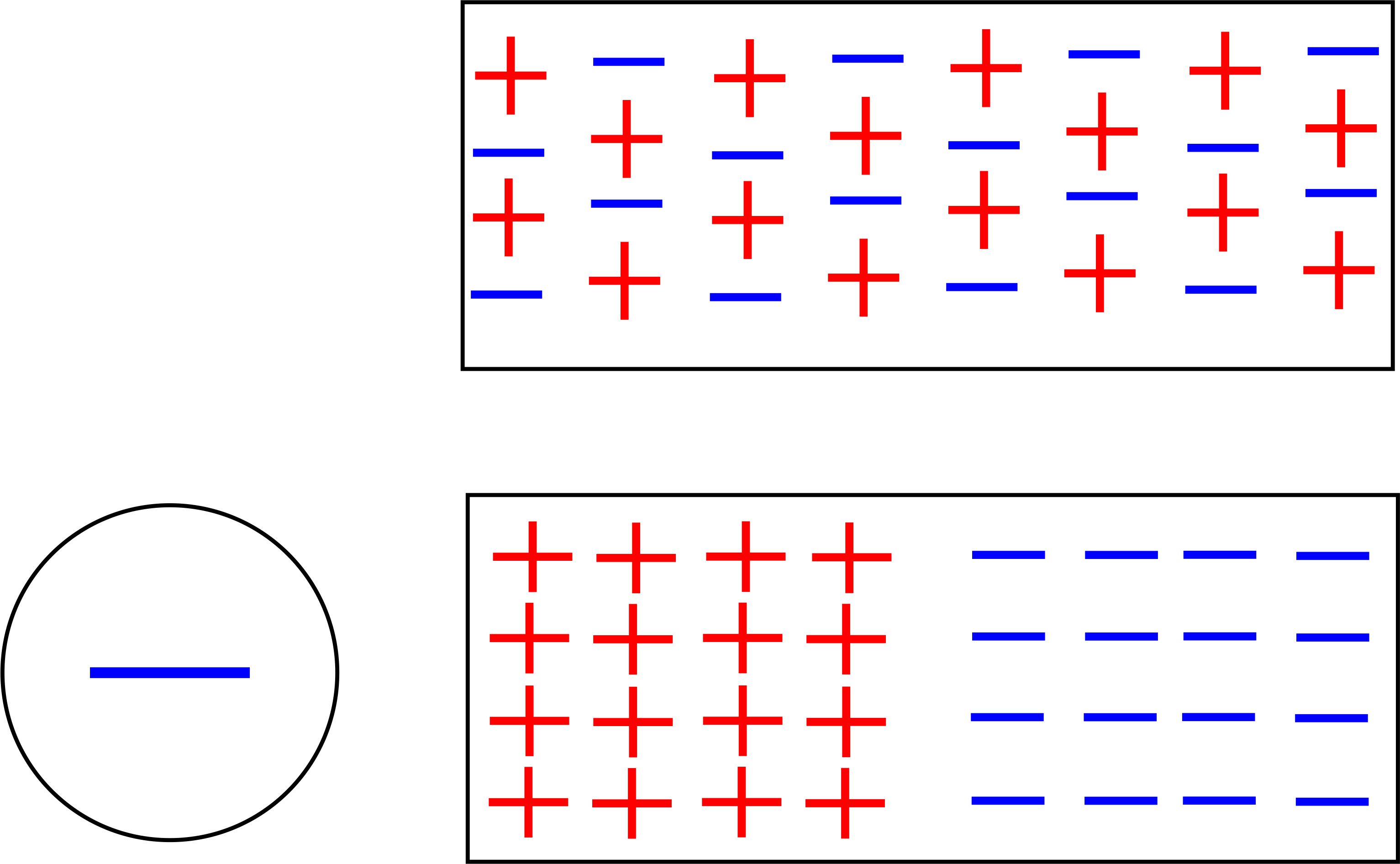
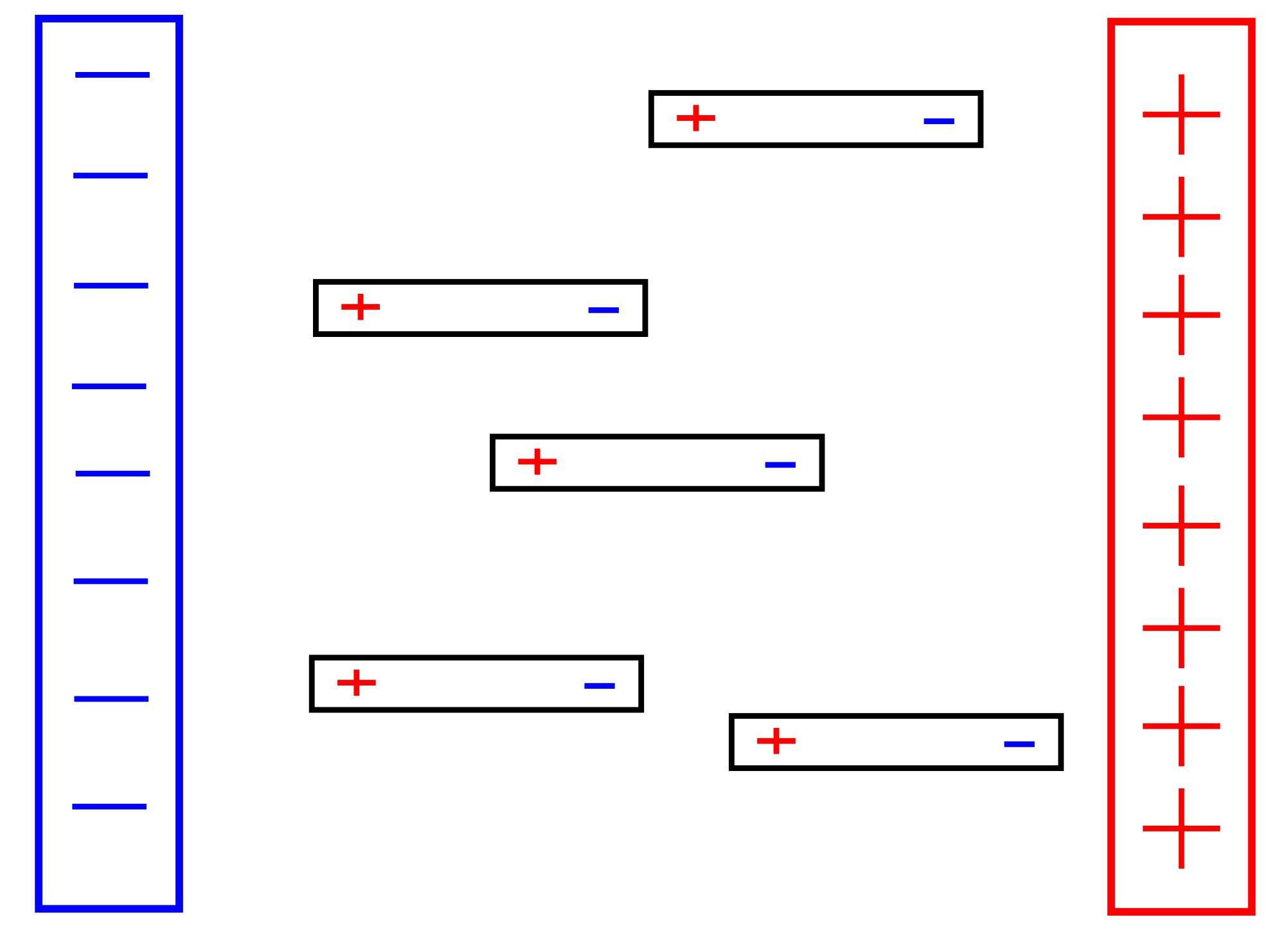
Man erkennt, dass es sich um eine vektorielle Größe handelt, die also eine Richtung aufweist. Die Richtung von E stimmt mit der Kraft- richtung auf eine positive Probeladung überein. Feldlinienbilder Wie beim Magnetfeld versucht man jetzt auch Feldlinienbilder des elektrischen Feldes aufzustellen. Man benutzt hierzu Dipole. Meist geht es um Dipole, die durch Influenz entstehen. Influenz bedeutet, dass das äußere Feld im Inneren des Dipol- Körpers die vorhandenen Ladungen verschiebt. Nehmen wir an, wir haben einen negativ geladenen Körper vorliegen und wir geben in das elektrische Feld einen neutralen Metallstab. Dann werden sich im Metallstab die frei beweglichen Elektronen (negativ) aufgrund der Abstoßung zum Ende bewegen, welches möglichst weit weg ist vom geladenen Körper, so dass auf der dem Körper zugewandten Seite die positiven Atomreste zurückbleiben. Im Dipol-Körper haben sich die zunächst homogen verteilten Ladungen durch die Anwesen- heit des geladenen Körpers jetzt neu verteilt. Es befinden sich Ladun- gen an den Enden des Metallstabes. Man spricht von einem elektri- schen Dipol. Die folgende Abbildung zeigt sehr schematisch die Influenz in einem metallischen Dipol:
Ein solcher Dipol richtet sich in einem elektrischen Feld entlang der Feldlinien aus. Versuchsablauf: (leider nur als Text, ich habe kein passendes Video
gefunden bzw. selber aufgenommen; wer ein Video parat hat, soll bitte Kontakt mit mir aufnehmen) Man
wählt als Dipol einfach einen Kupferstab aus einer elektrischen Leitung.
An diesen Kupferstab wird mittig ein Kunststofffaden ange- klebt,
an dem dann der Kupferstab hängt. Mit diesem Aufbau geht man jetzt in die verschiedenen
Anordnungen, in denen sich dann der dreh-bar aufgehängte Kupferstab
ausrichtet. Hinweis: In den meisten Fällen wird das Feldlinienbild
mittels Grießkörnern oder Kunst- stofffasern aufgenommen. Gießkörner und Kunststoffasern
sind Isolatoren, d.h. hier können sich nicht frei bewegliche
Elektronen verschieben. Es gibt also nur Verschiebungen der Elektronen
innerhalb der Atome. Die Atome selber werden zu Dipolen. Hierzu hier ein paar Links: - 1.)
sehr schönes Video zu Versuchen mit Gießkörner mit zusätzlichen Erklärungen -
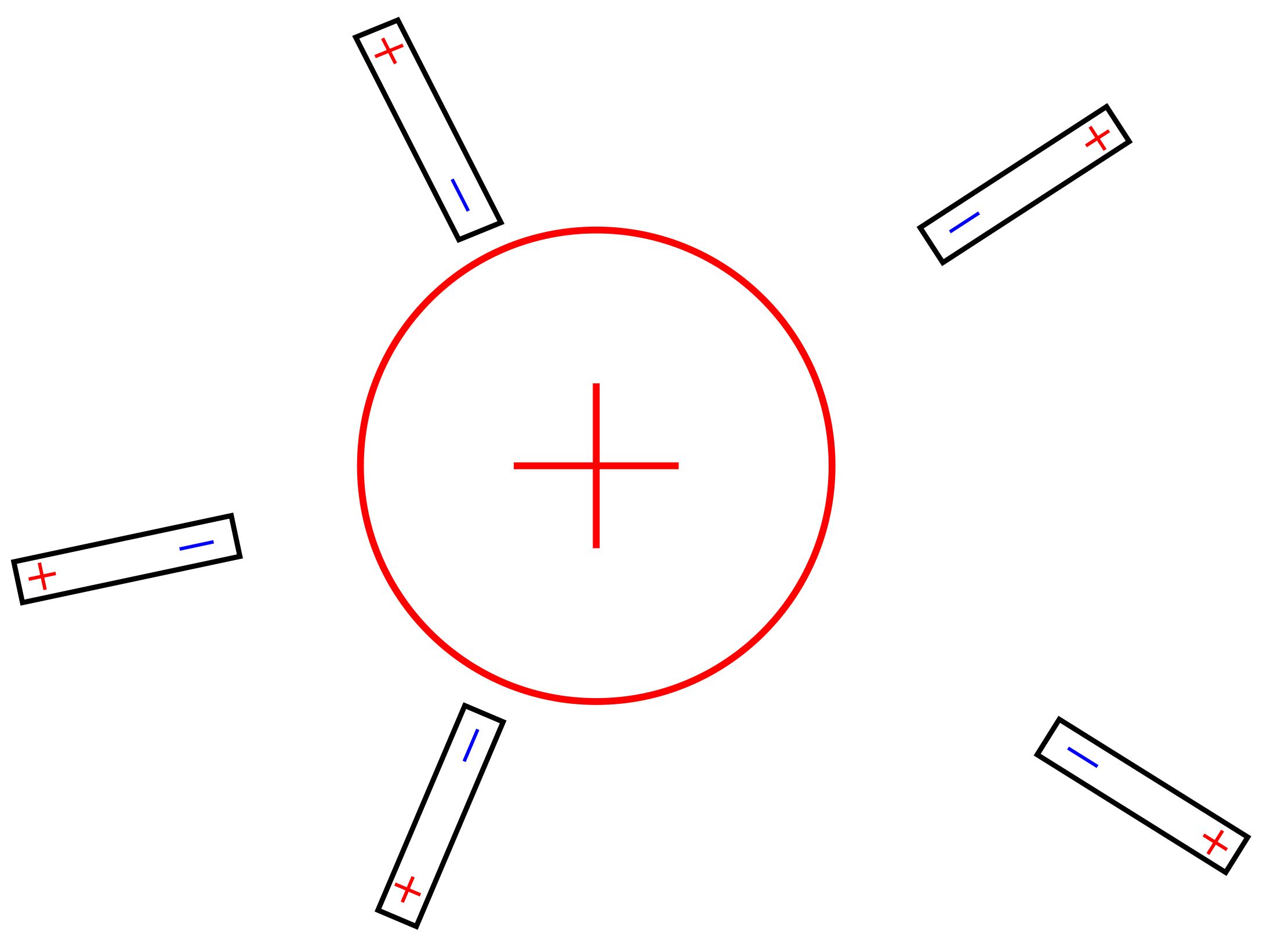
2.) hier ein Video mit Kunststofffasern Die folgenden Abbildungen zeigen die Ausrichtung des
Dipols an verschiedenen
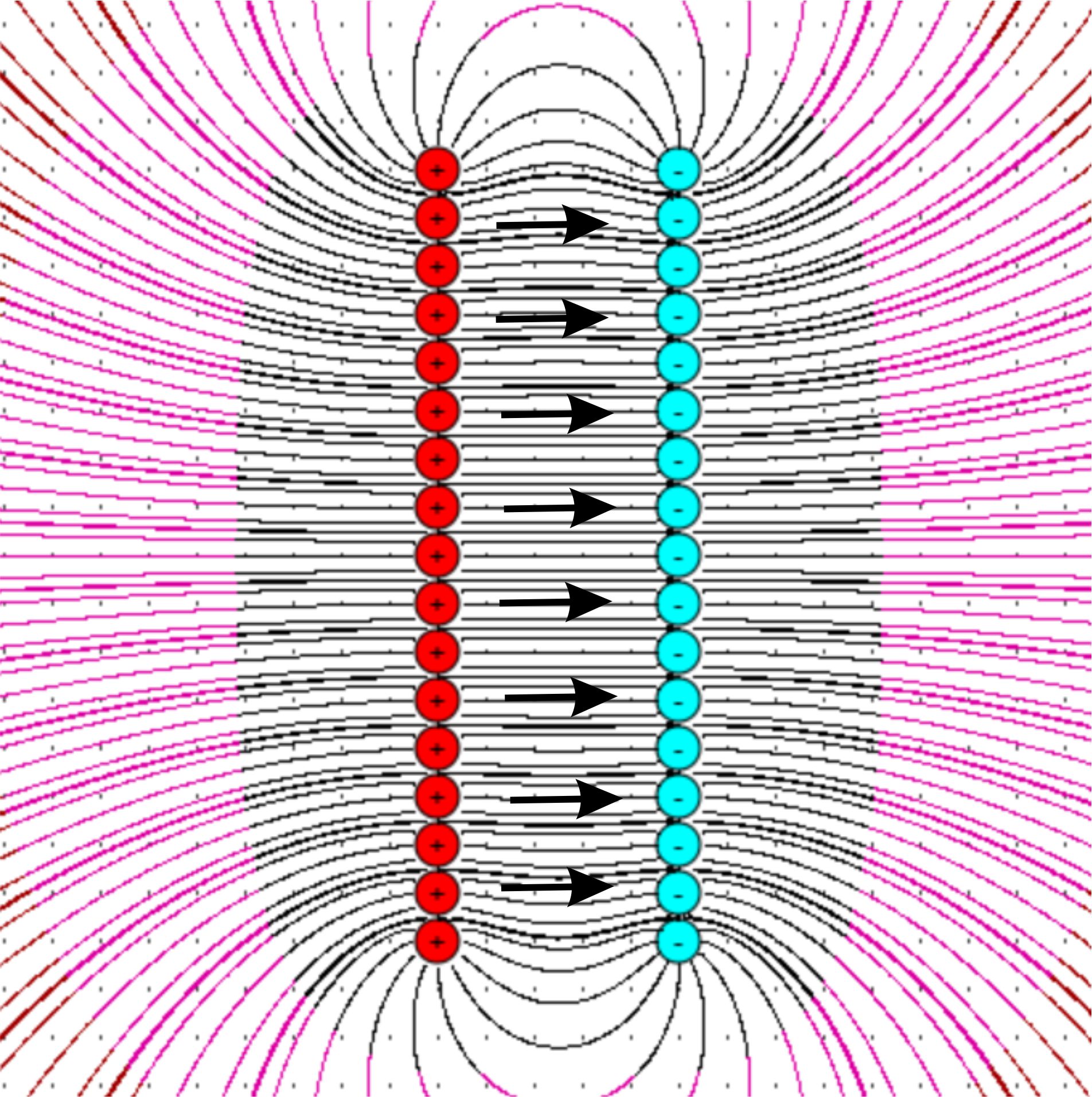
Positionen in der Nähe einer geladenen Kugel bzw. zwischen
zwei unterschiedlich geladenen Platten (Plattenkondensa-tor).
Programm zur Erstellung von
Feldlinienbildern Es gibt
ein uraltes Programm von Prof Dr. Raimund Girwidz,
mit dem man
solche Feldlinienbilder zeichnen kann. Das Programm verwendet die
Überlagerung vieler Radialfelder, um das Gesamtfeld zeichnen zu können.
(Hinweis:
Wir kommen später noch zum Coulomb-Gesetz, mit dem das Programm arbeitet. Das Programm konnte man käuflich erwerben. Es
läuft aber mit den modernen Be- triebssystemen nicht mehr. Da es für die alten
Betriebssysteme (MS-DOS) geschrieben wurde, ist es auch nicht besonders komfortabel in der
Handhabung) Herr Girwidz stellt das Programm jetzt auf der Seite der Uni
München im
Internet zur Verfügung (
Link zum Programm ) Ich habe
mit diesem Programm einmal einige Feldlinienbilder zeichnen lassen
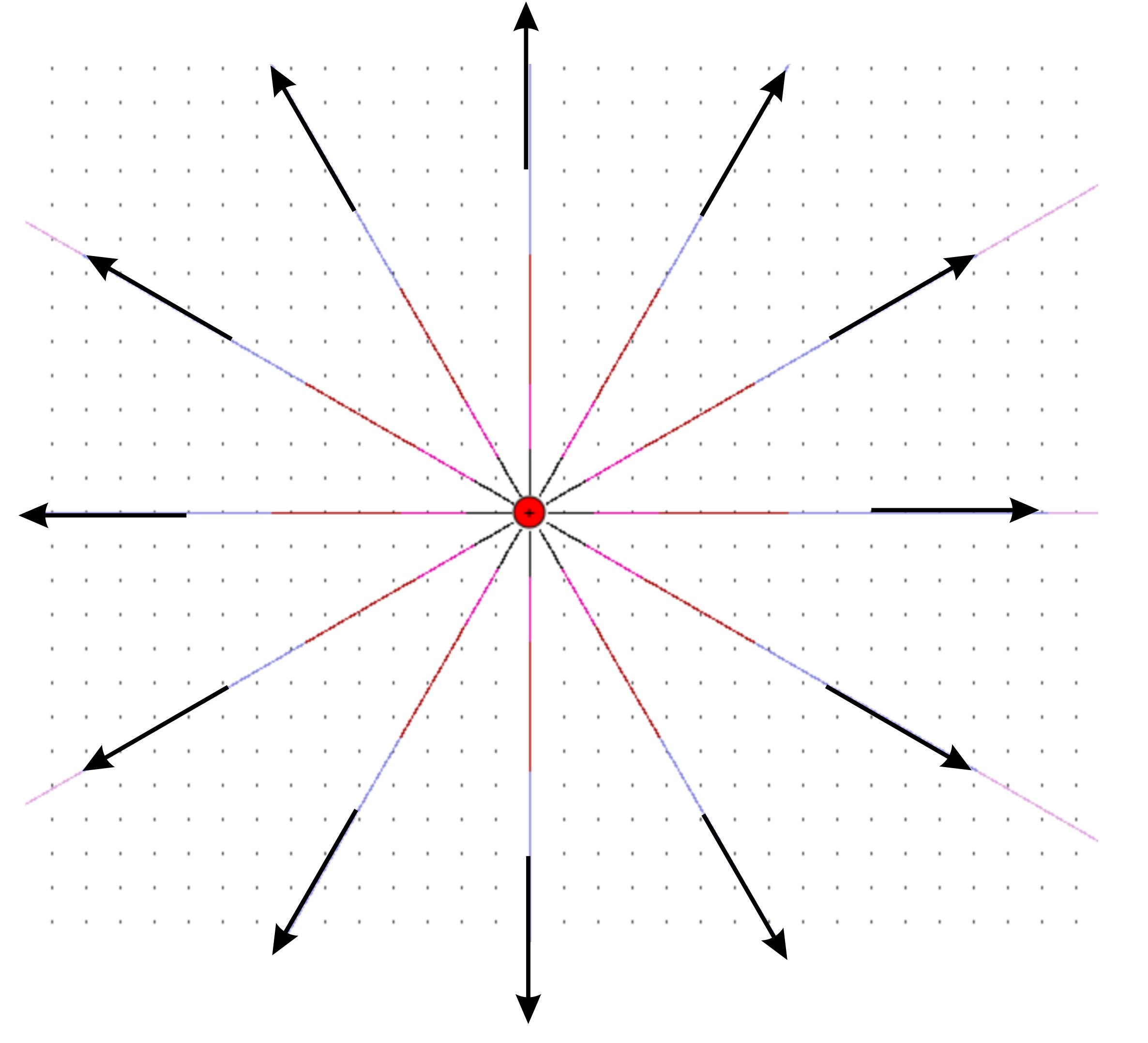
und die Feldlinienrichtung nachträglich zusätzlich eingetragen. Hinweis: Neben der Feldliniendichte macht hier auch die
Farbe eine Aussage über die Größe der Feldstärke!
Man
erkennt sofort, dass die Feldlinienstruktur mit den Versuchser- gebnissen
übereinstimmt. Komplexe Feldstruktur, wenn
mehrere Ladungen vorliegen Wenn mehrere Ladungen vorliegen, ergibt sich das Gesamtfeld als die Überlagerung der Einzelfelder. Die Konstruktion der Feldstruktur geht im Prinzip wie bei
der Überlagerungen von Kräften. (Stichwort: Kräfteparallelogramm,
vektorielle Addition) Folgende Abbildung zeigt, wie man hier „händisch“ vorgehen muss.
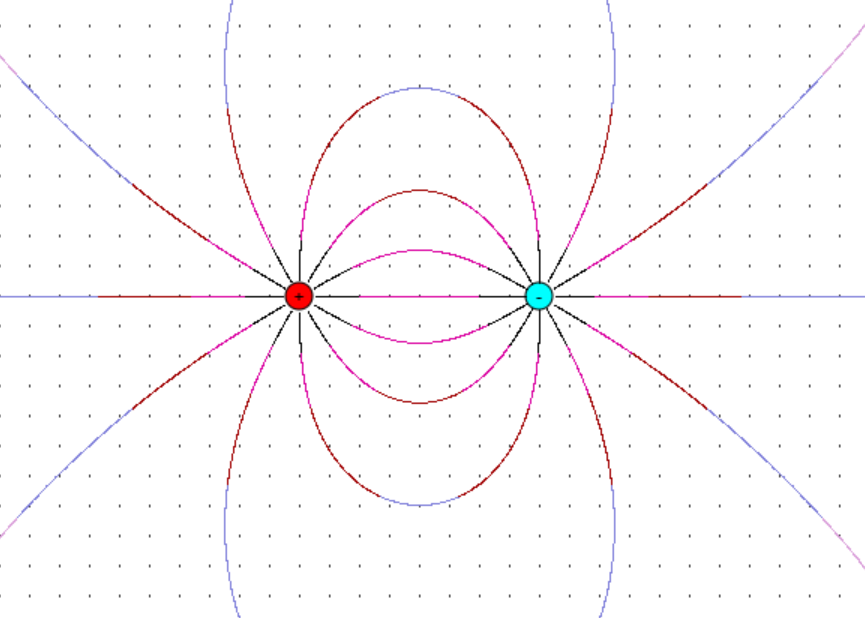
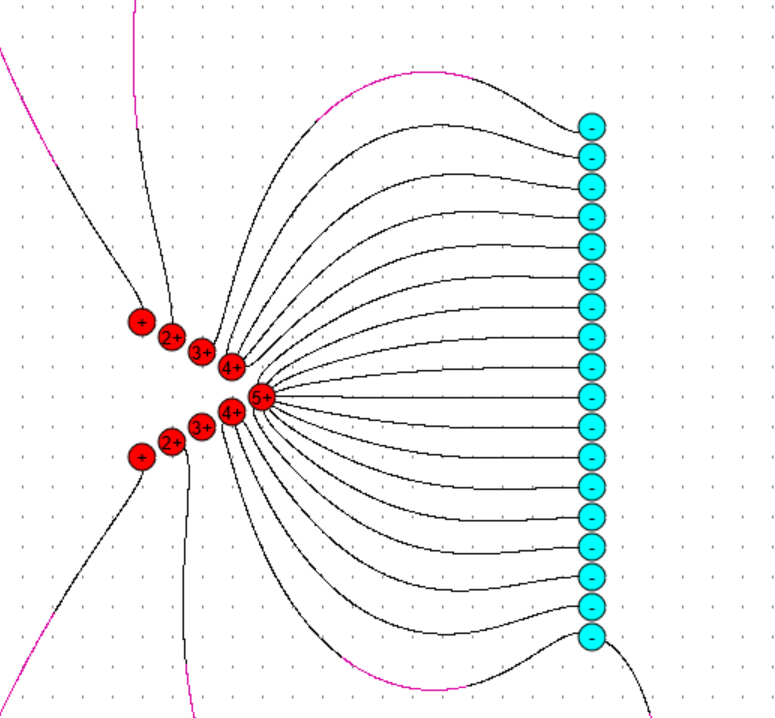
Das Programm von Herrn Girwidz rechnet dies sofort aus und gibt dann das Ergebnis graphisch aus. Hier die
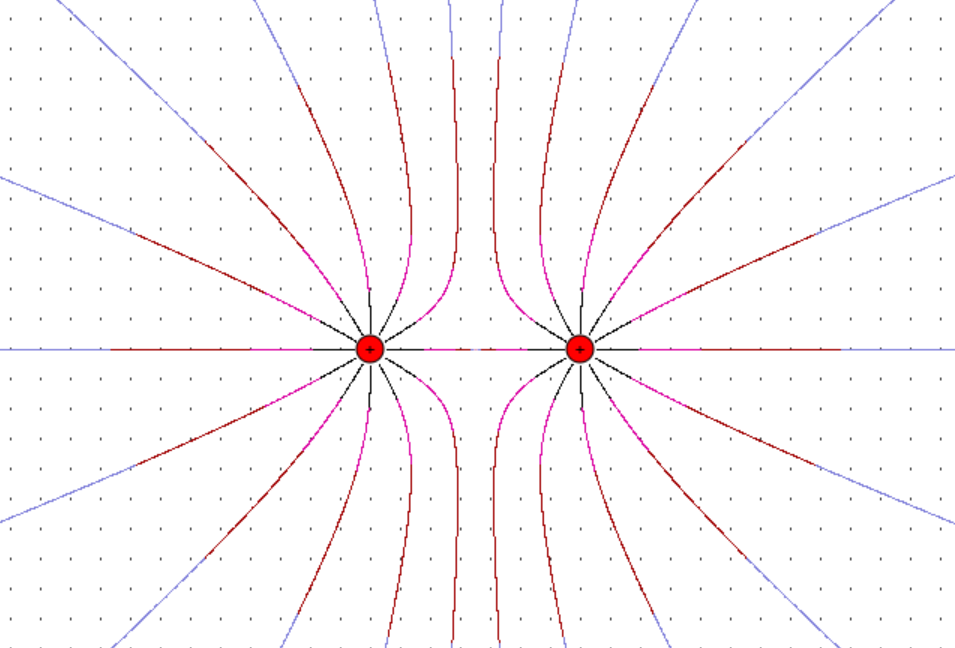
Ergebnisse für ungleiche und gleiche Ladungen.
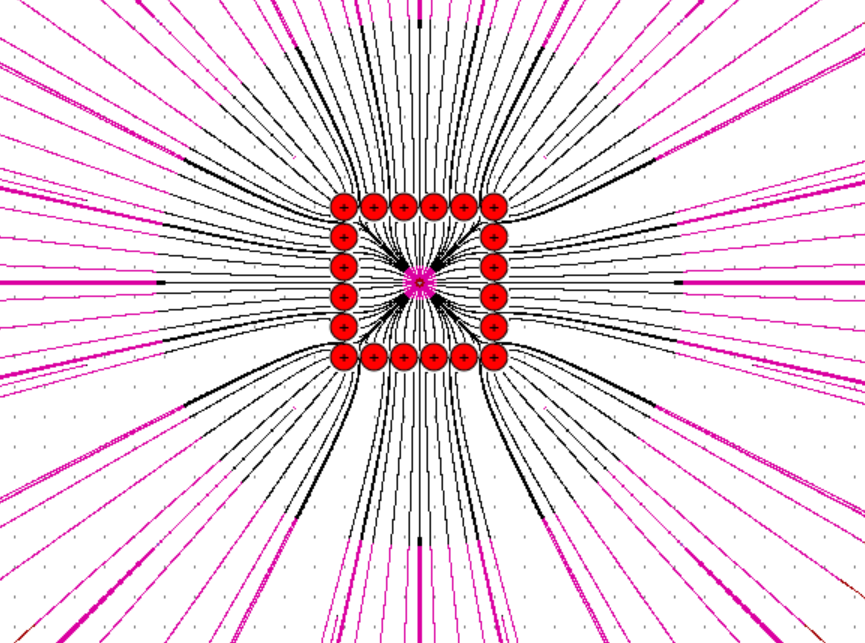
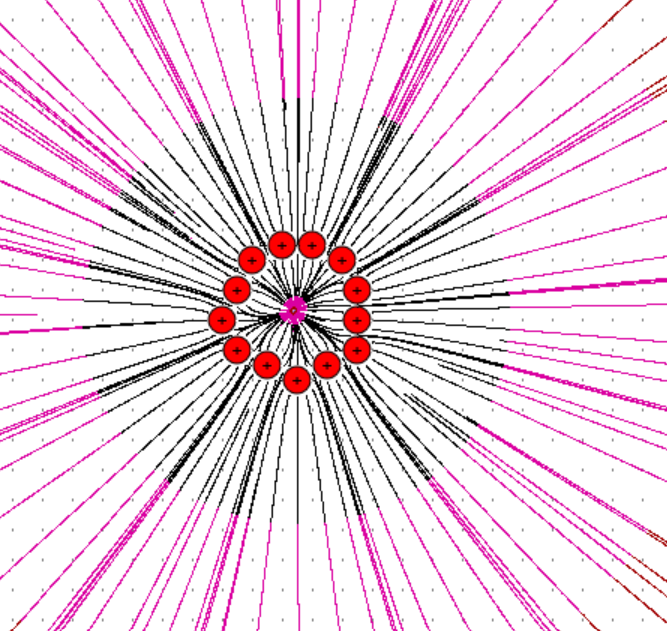
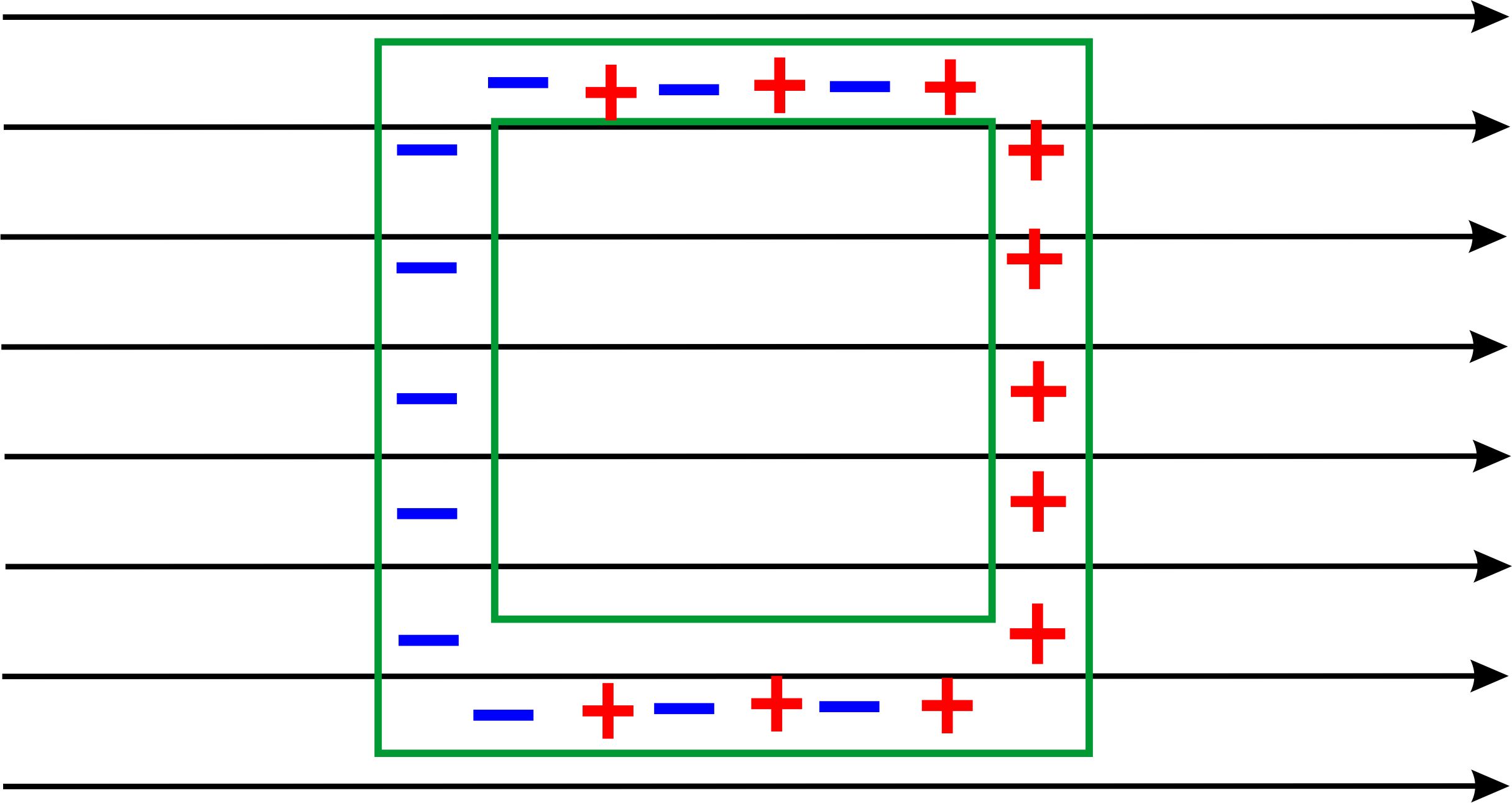
Faraday−Käfig Die Überlegungen zum zweiten Fall (Feld zweier gleich geladener Punkte) legt nahe, dass in einem geladenen Hohlkörper ein feld- freier Raum vorliegt. Man spricht von einem Faraday-Käfig. Mit dem Programm von Girwidz kann man diesen Fall nur stark eingeschränkt zeigen, da das Programm nicht 3D-Bilder zeichnet und die Anzahl der Ladungen beschränkt ist. Ich habe es mal mit einem quadratischen Hohlraum und einem Hohl- ring (schwer zu konstruieren, da man die Ladungen nicht beliebig setzen kann) versucht. In beiden Fällen sieht man noch Felder im Inneren. In der Mitte aller- dings stark abgeschwächt.
Exakte Berechnungen werden mit dem Gaußschen Gesetz in ein- schlägigen Büchern (Tipler; Giancoli) meist für eine Hohlkugel durch- geführt. Wir verzichten hierauf, weil es kein Stoffinhalt der S II ist. (Link zu einer Darstellung
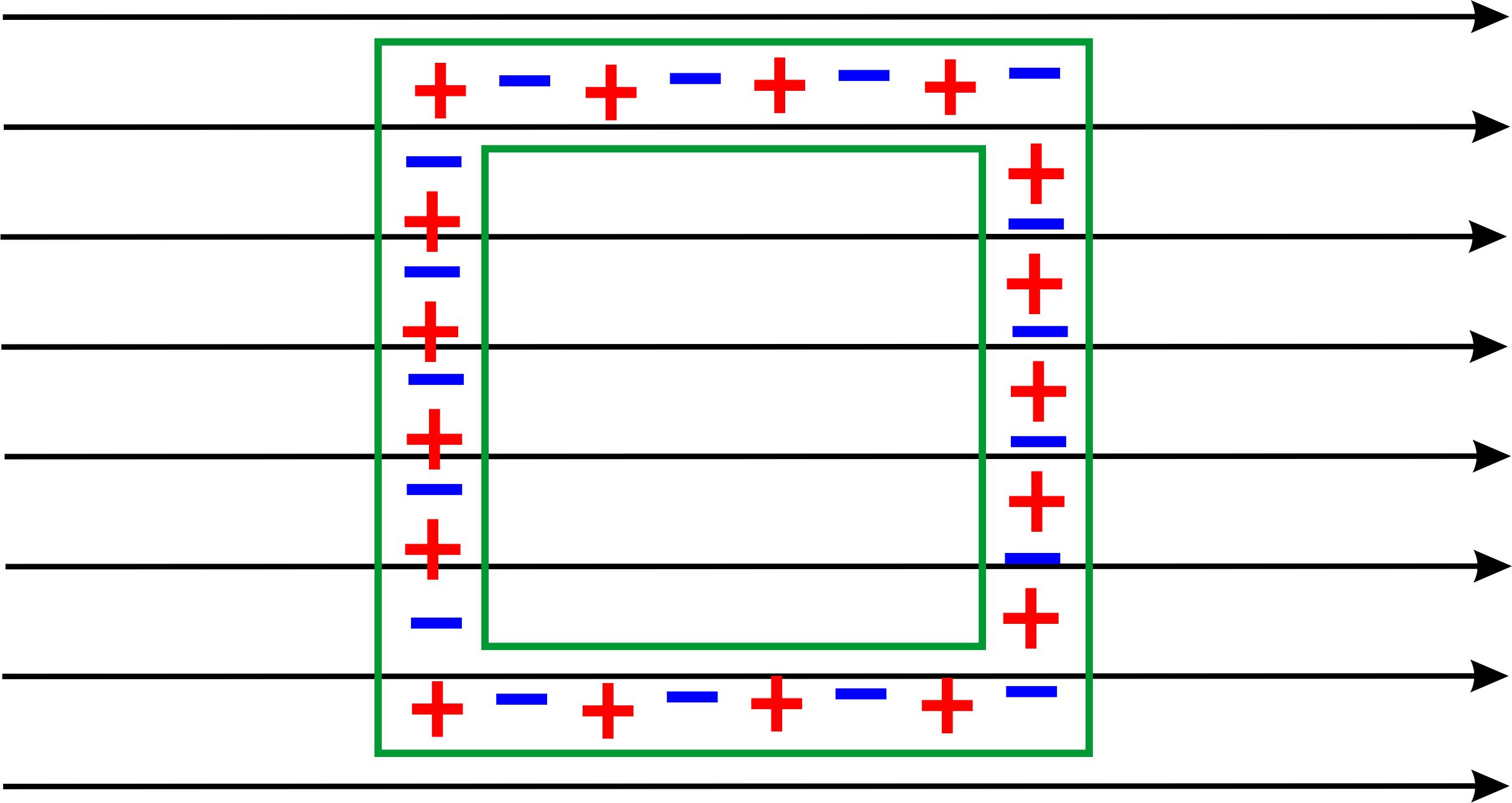
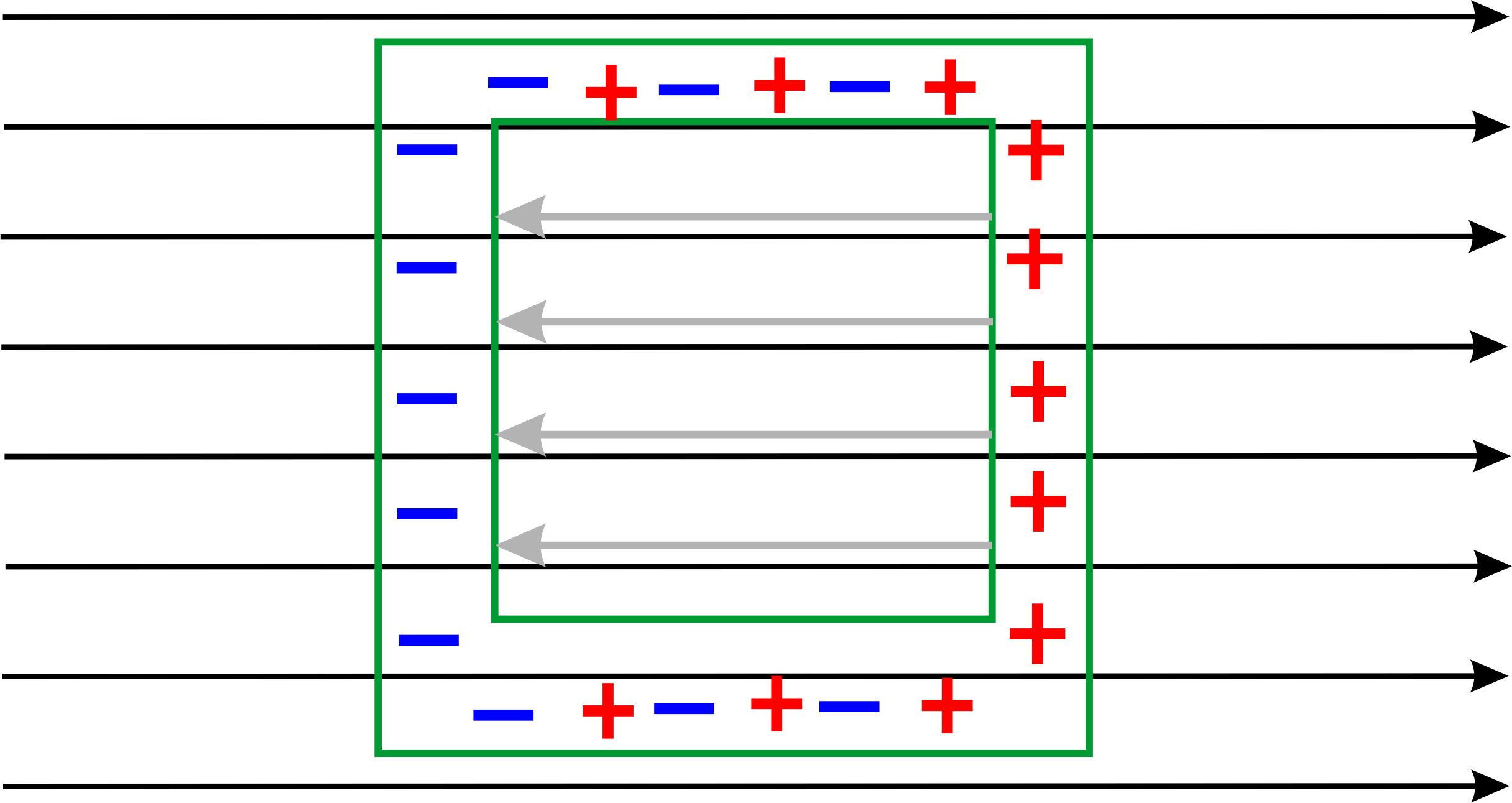
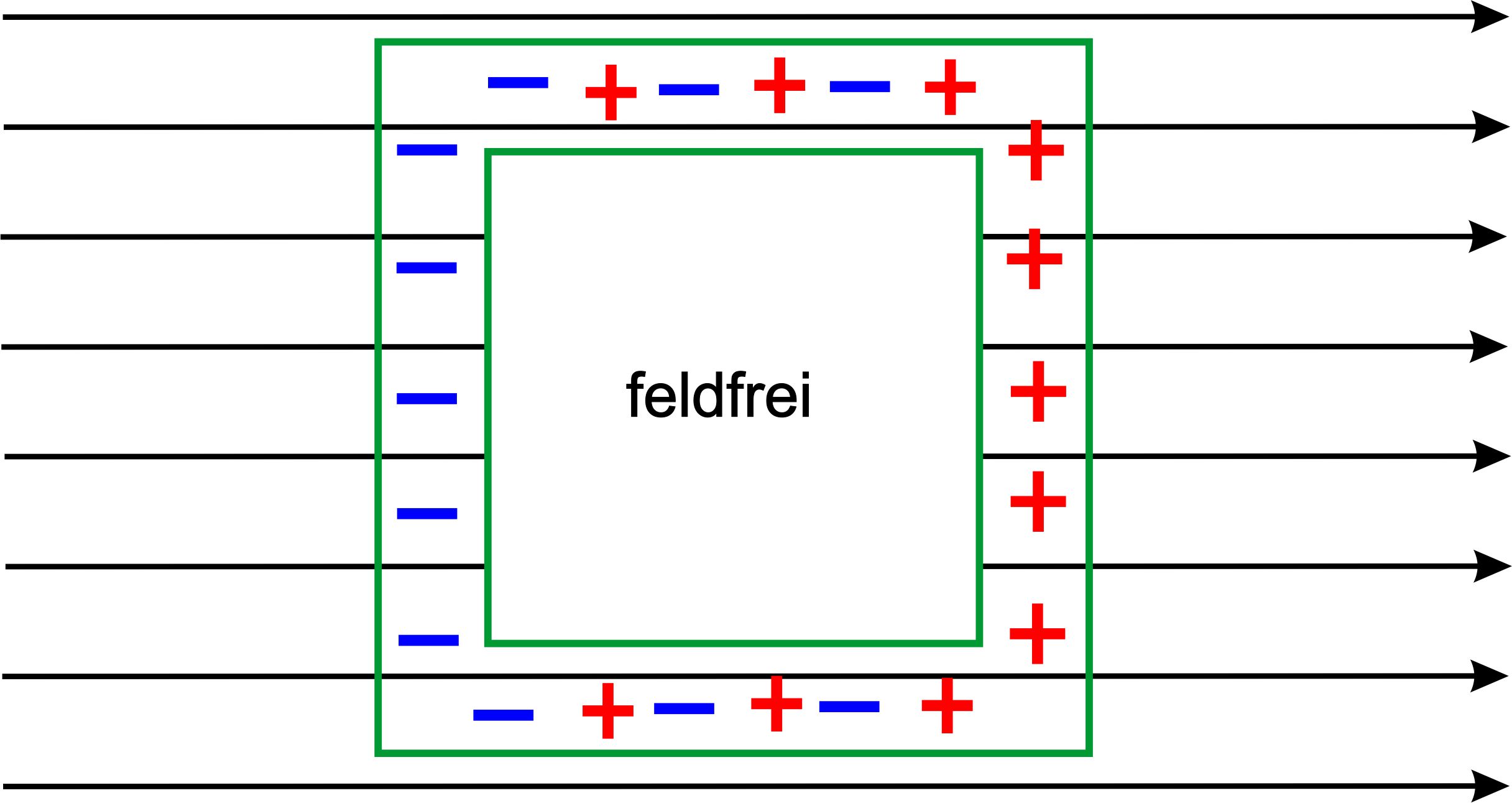
im Internet zur Hohlkugel) Falls der Hohlraum nicht geladenen ist, sondern sich nur in einem elektrischen Feld befindet, wird oft mit Influenz argumentiert. Folgende Serie von Abbildungen soll dies erklären.
Wenn man
sich in einem Faraday-Käfig befindet, ist man vor elek- trischen
Feldern, vor allem Blitzen, geschützt. Bei einem Gewitter sollte
man daher möglichst einen solchen Raum (Auto, Haus) auf- suchen. Video zum Thema „Faradaykäfig“
Quarks&Co hat das Thema „Blitz und Gewitter“
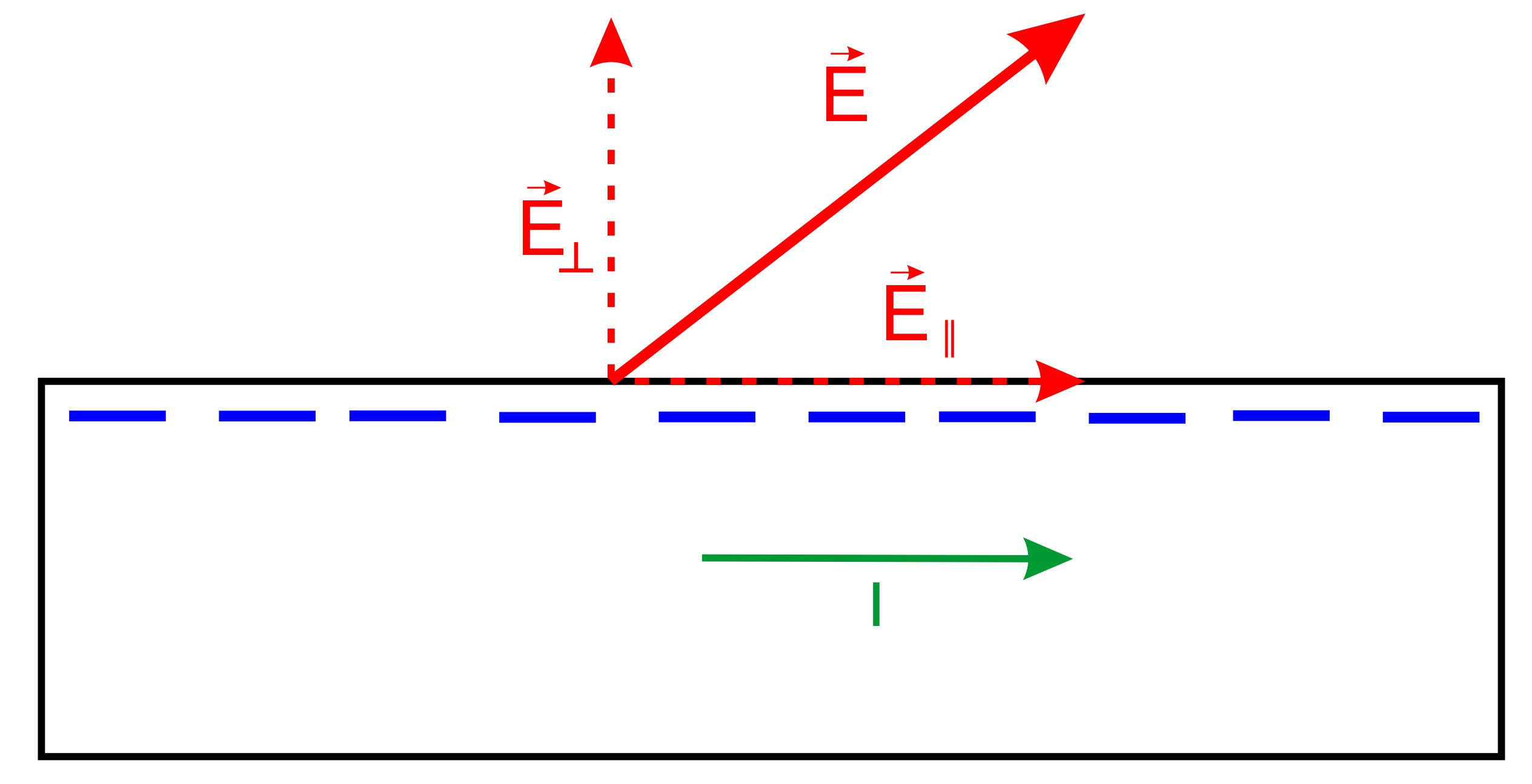
zweimal behandelt. - https://www.youtube.com/watch?v=SZHwWgY0NBM - https://www.youtube.com/watch?v=JFBxCZtjp6I Zusatzinformationen 1.) Feldlinienrichtung an der Oberfläche von Ladungen An der Oberfläche von geladenen Körpern verlaufen die Feldlinien senkrecht zur Oberfläche, falls Elektrostatik vorliegt, also kein Strom fließt. Um dies zu erläutern, beziehen wir uns auf folgende Abbildung.
Falls die Feldlinie nicht senkrecht auf der Oberfläche stände (wie in der Abbildung), dann gäbe es eine parallele Komponente E║, die für einen Stromfluss I sorgen würde. Dies hieße aber, dass kein elektro- statischer (ohne Stromfluss) Fall vorläge. Es gilt also:
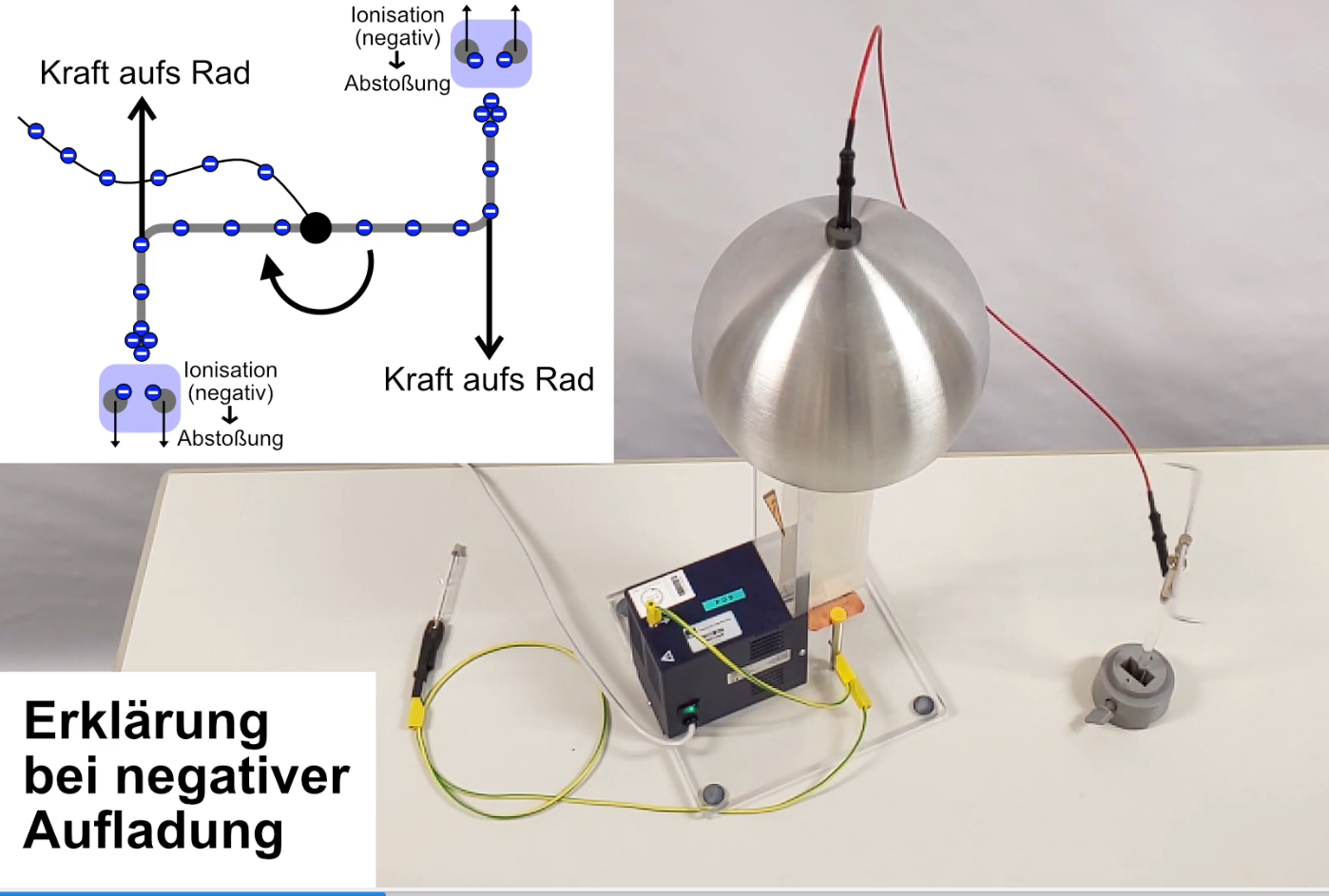
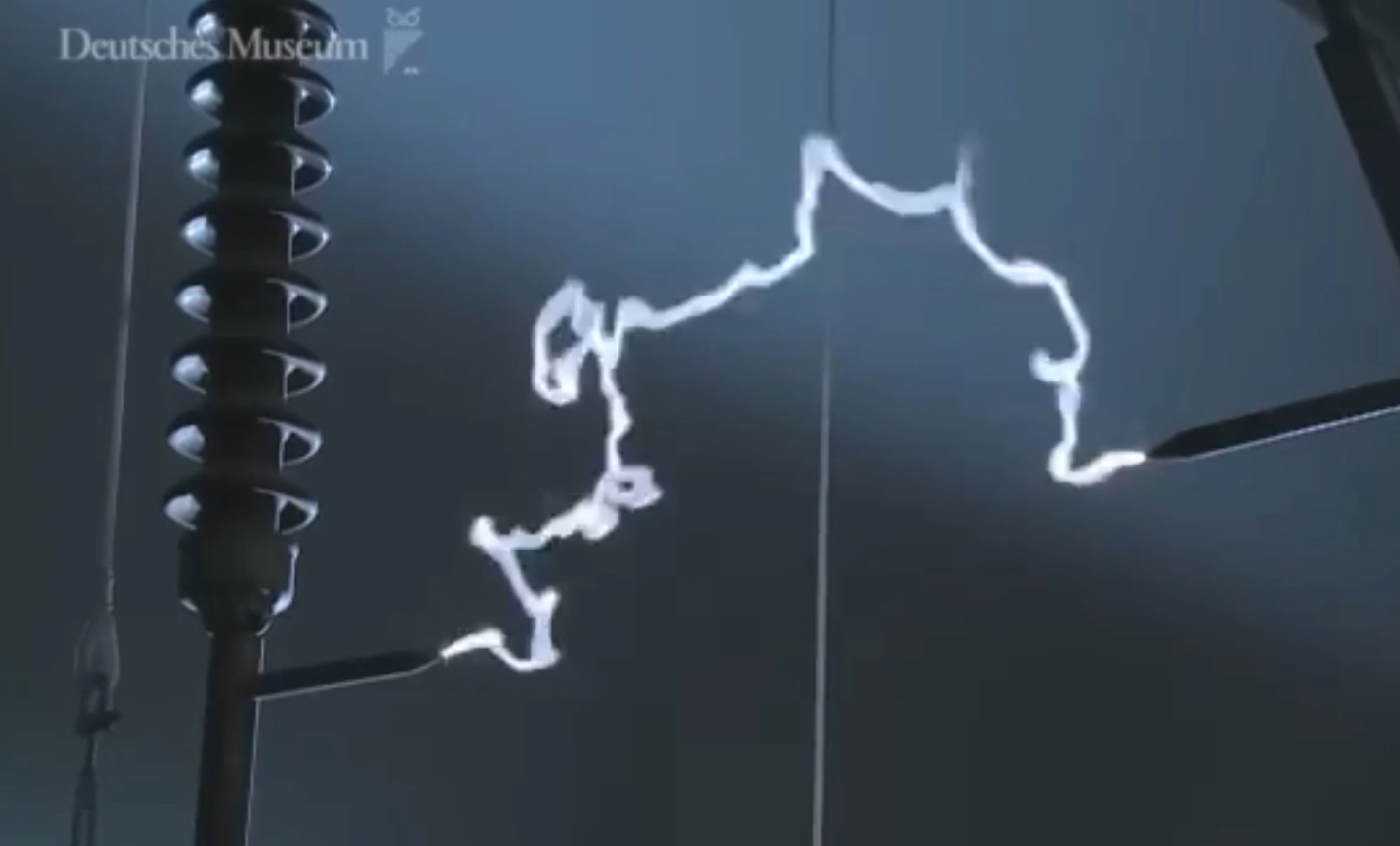
2.) Feldverlauf an einer Spitze An einer leitfähigen Spitze sammeln sich besonders viele Ladungen an. Dies führt zu einer extrem hohen Feldstärke, so dass an diesen Stellen bevorzugt die Entladungen oder Blitzeinschläge stattfinden. Mit dem
Programm von H. Girwidz ist dies nur sehr
eingeschränkt zu zeigen,
da man die Ladungen nicht beliebig auf der Zeichenfläche setzen
kann.
Videos zum Thema Spitzenentladung:
3. Unterschied zwischen elektrischen und magnetischen Feldern Wir haben schon in der Einführung gesehen, dass sowohl Magnete als auch Ladungen von Feldern umgeben sind. Man spricht vom magnetischen bzw. elektrischen Feld. Hinweis:
Zum Magnetismus (insbesondere zur Lorentzkraft) gibt es später noch ein
eigenes Kapitel. Ein grundlegender Unterschied zwischen magnetischen Feldern und elektrischen Feldern ist, dass elektrische Felder eine Quelle, also einen Anfang und ein Ende haben. Sie beginnen auf positiven La- dungen und enden auf negativen Ladungen, während Magnetfelder geschlossen sind, also keinen Anfang und kein Ende aufweisen. Man hat bisher keine Monopole gefunden, die magnetische Felder er- zeugen könnten. Wir halten also fest:
Hinweis:
Es geht hier um elektrische Felder, die durch Ladungen erzeugt werden. Im
Kapitel „Induktion“ findet man auch quellenfreie elektrische Wirbelfelder.
|