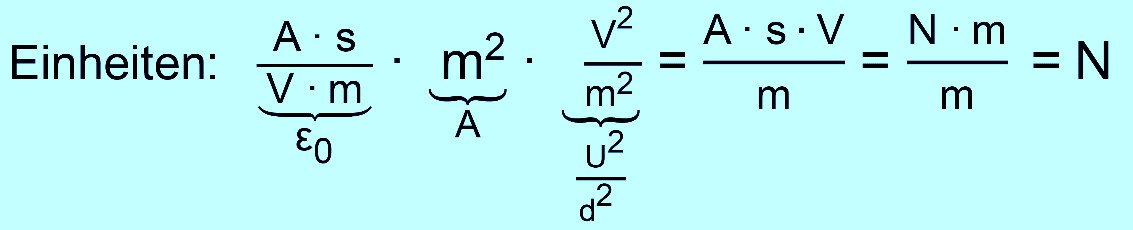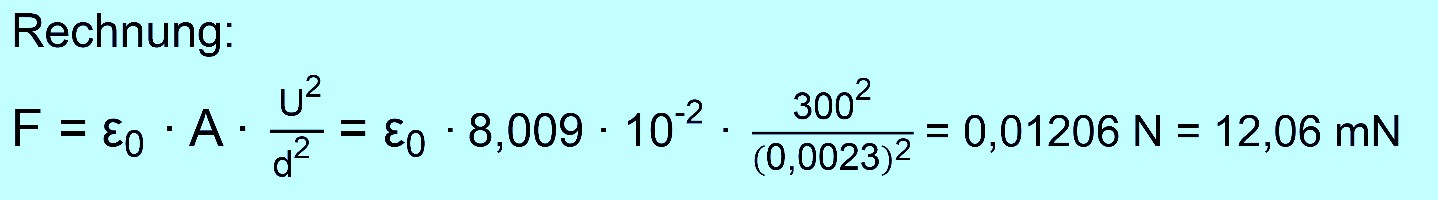|
Kraft
zwischen Kondensatorplatten Analog
zum Coulombschen Gesetz soll in diesem Kapitel eine
Formel für die
Kraft aufgestellt werden, die auf die Platten eines Plattenkon- densators
einwirkt. Warum
muss es eine solche Kraft geben? Jede Platte eines Konden- sators
befindet sich in einem elektrischen Feld. Deshalb muss nach der
Formel F = E ∙ Q eine Kraftwirkung auf die Platten vorliegen. (s. theoretische Herleitung der Formel) Wir
wollen uns zunächst einen Versuchsaufbau ansehen, mit dem man die
Kraft auf eine Kondensatorplatte messen kann. Es werden danach
Messwerte aufgenommen und ausgewertet. Wir erstellen auf- grund der
Auswertung eine provisorische Formel auf, die dann durch die
theoretische Herleitung der Formel präzisiert wird. Am Schluss steht
dann die eigentliche Formel zur Bestimmung der Kraft auf eine Kondensatorplatte.
Zunächst
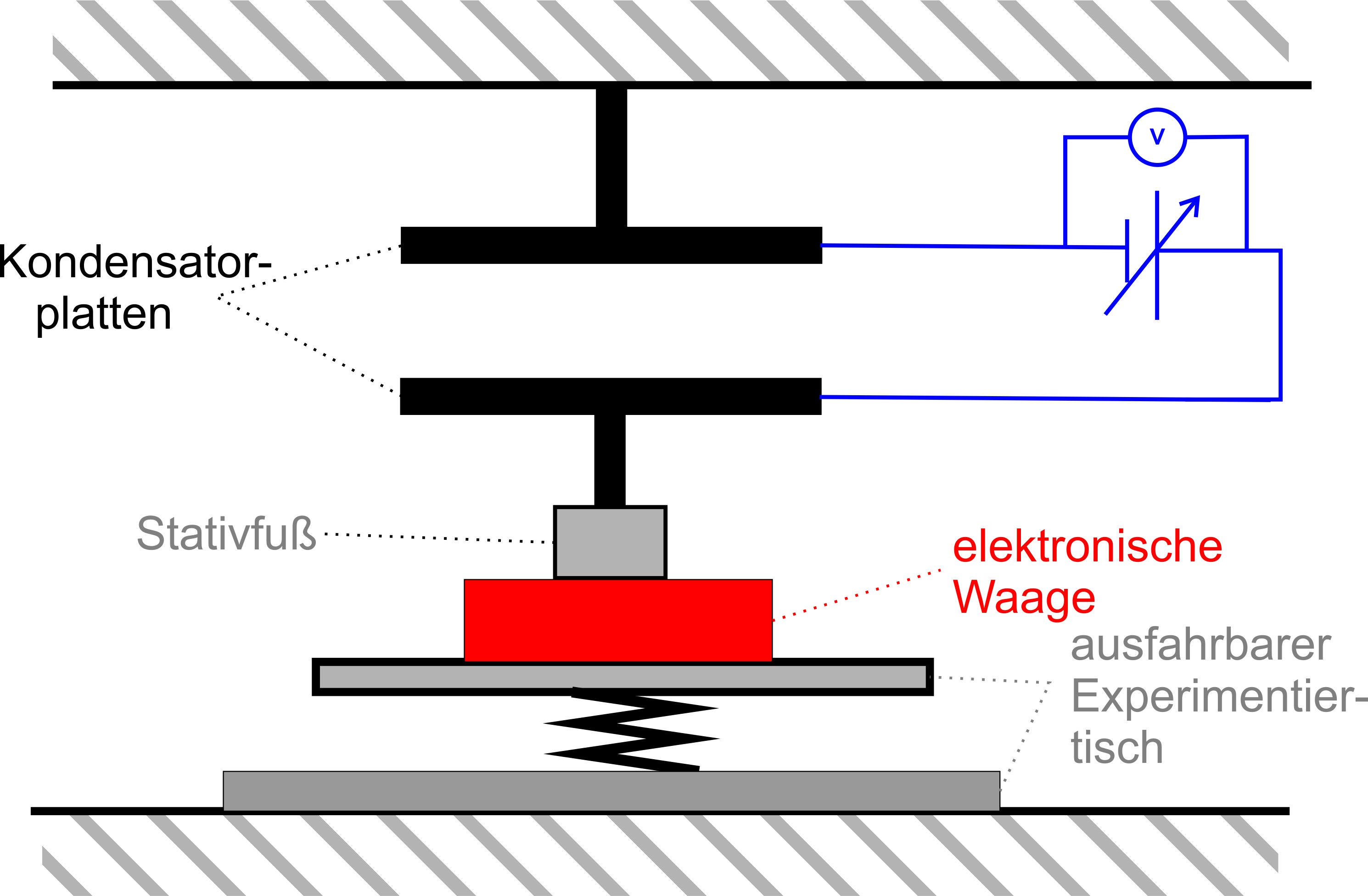
zum Versuchsaufbau, der in folgender Abbildung dargestellt wird.
Eine
Kondensatorplatte (hier die obere) ist starr befestigt. Die untere Platte
befindet sich mittels eines Stativfußes auf einer elektronischen Waage.
Diese Waage liegt auf einem ausfahrbaren Experimentier- tisch,
so dass der Abstand der Platten verändert werden kann. Dieser Abstand
kann mit einem Maßstab gemessen werden. Gleichzeitig liegt an
den Platten eine Spannung an, die regelbar ist und über das Voltmeter
gemessen wird. Wenn
eine Spannung angelegt wird, wird die untere Platte von der oberen
angezogen. Die Waage, die auf Null justiert wurde, zeigt jetzt einen
Ausschlag. Die Masse des aufliegenden Aufbaus (untere Platte +
Stativfuß) hat abgenommen. Hieraus lässt sich die Anziehungskraft mit F =
m ∙ g berechnen. Messwerte und Auswertung Es
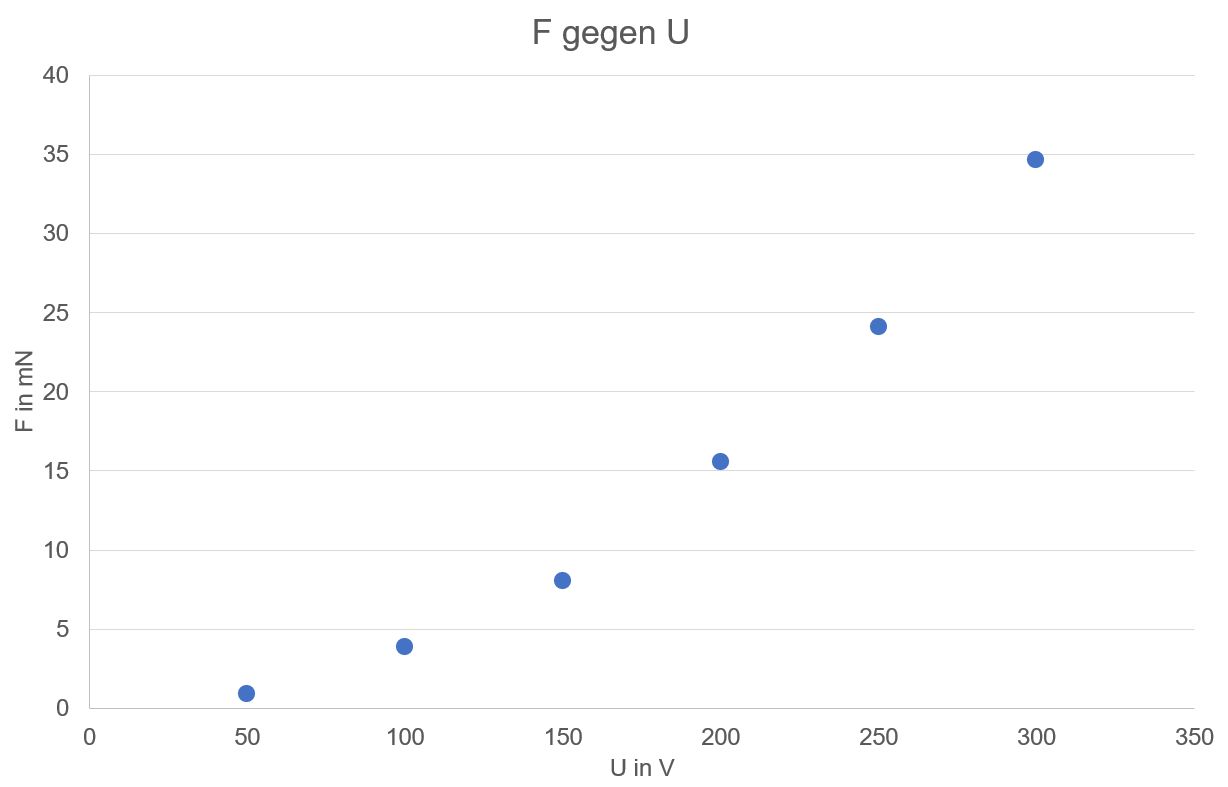
werden zwei Messreihen durchgeführt. Einmal wird der Abstand d konstant
gehalten und U verändert. Im anderen Fall bleibt U konstant und d
wird geändert. Bei jeder Messung wird der Masseverlust be- stimmt
und in F umgerechnet. Es
ergeben sich folgende Messwerte: 1.
Messreihe: d=konstant≈0,3 mm, A = konstant = 8,009 ∙10−2
m2
2. Messreihe:
U = 300 V = konstant, A = konstant = 8,009 ∙10−2 m2
Die
Auswertung mit Excel ergibt:
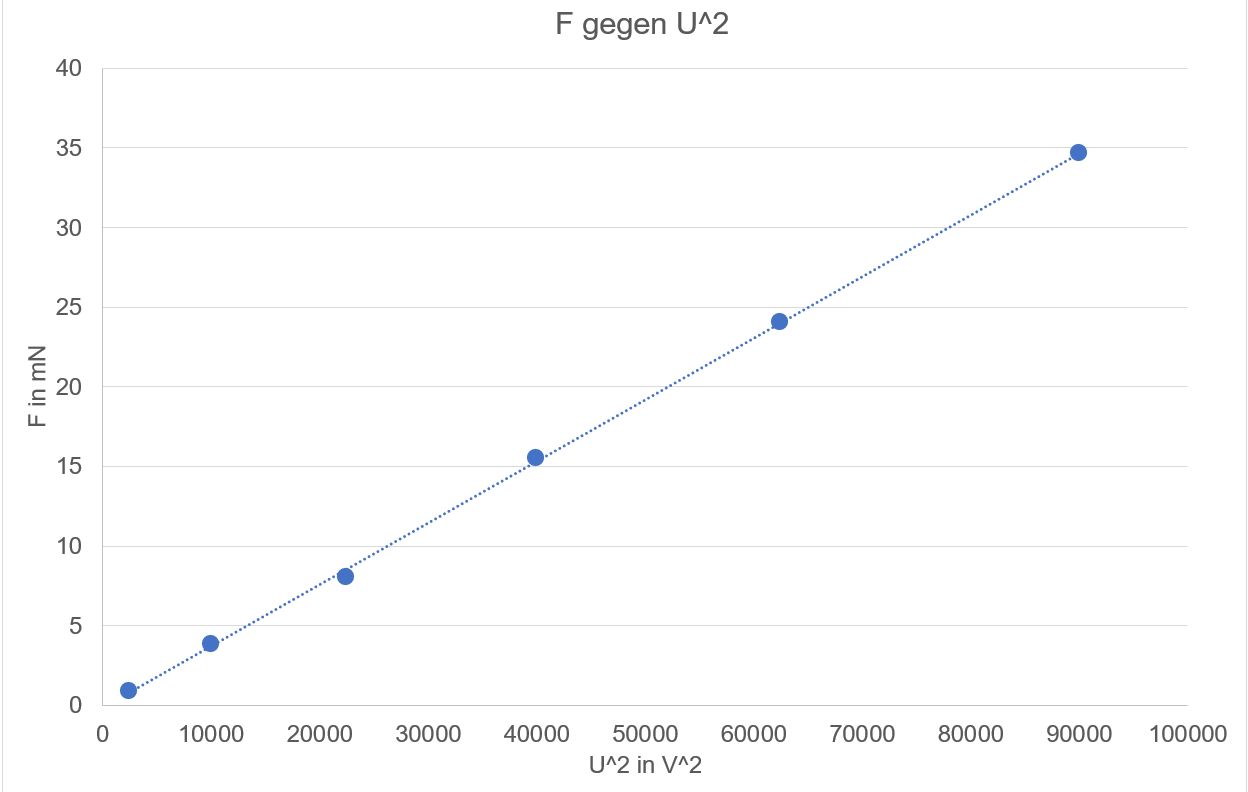
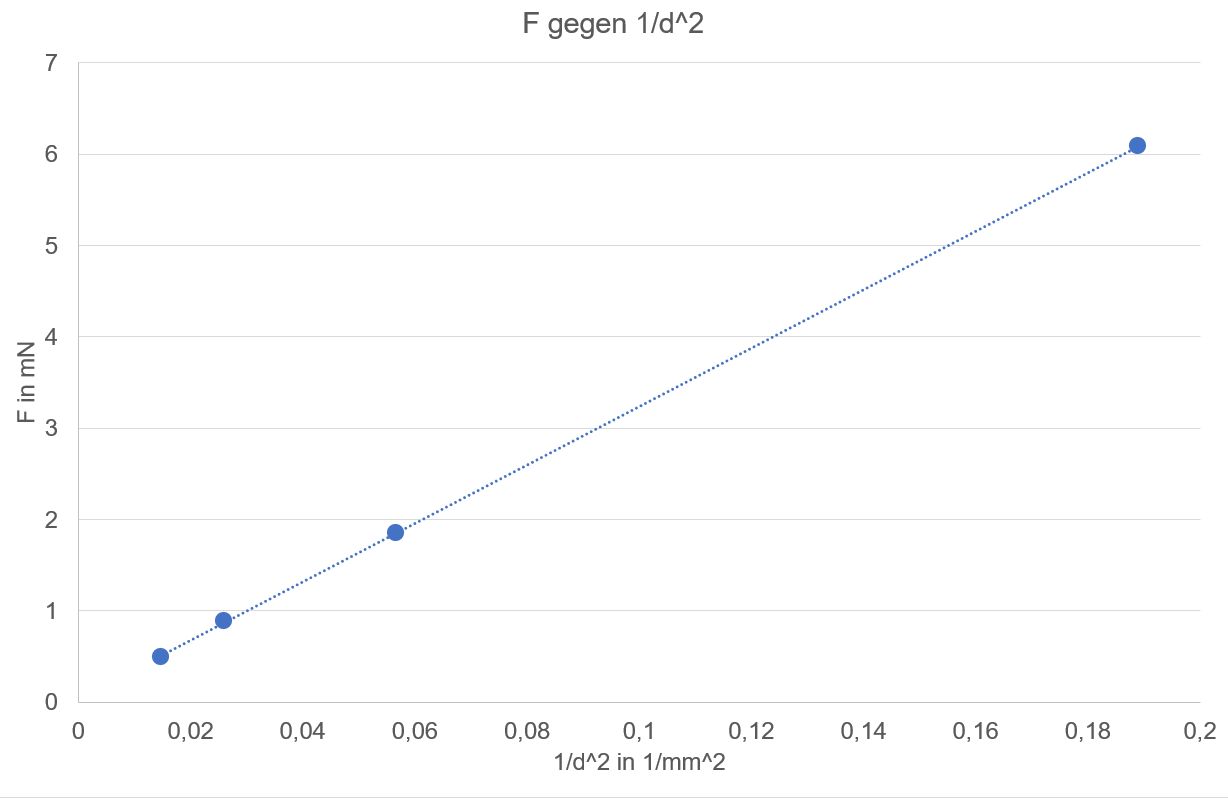
Da im
Diagramm F gegen U2 eine Ursprungsgerade auftritt, gilt F
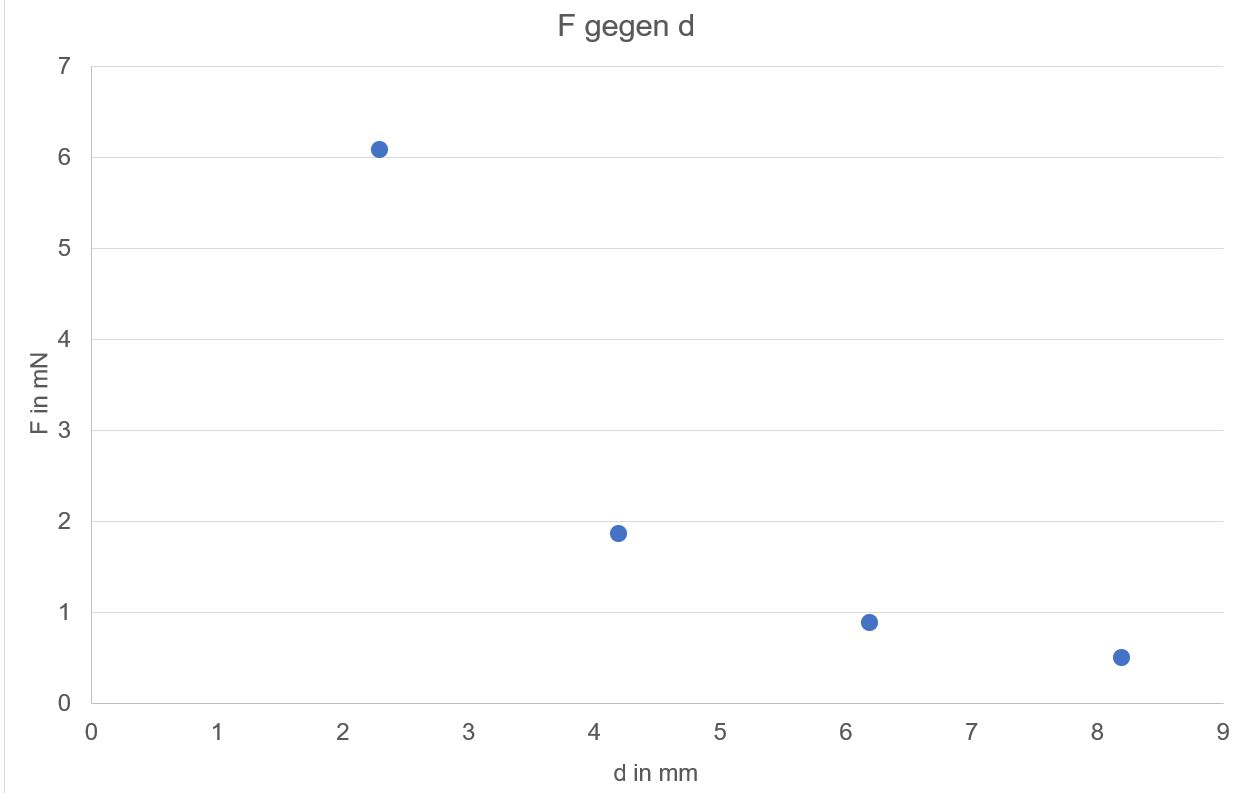
Für den
Zusammenhang zu d gilt:
Hier
gilt also: F
Wir
können ohne große Messungen wohl davon ausgegehen,
dass auch
noch gilt: F
Für den
Gesamtzusammenhang ergibt sich somit:
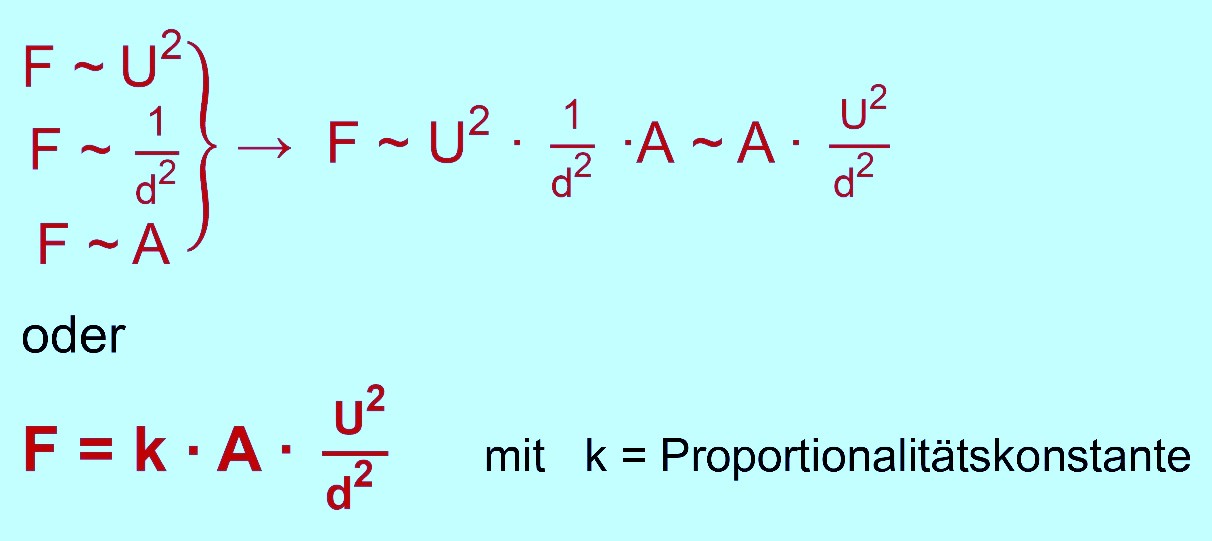
Theoretische Herleitung der Formel Man kann
die Formel auch theoretisch herleiten, um ein besseren Blick
auf die Proportionalitätskonstante zu bekommen. Es ergibt sich dann:
Wir
kontrollieren zunächst einmal nach, ob dies von den Einheiten passen
würde.
Von den
Einheiten würde es passen. Es könnte natürlich immer noch ein
Faktor ohne Einheit dazukommen. Deshalb
rechnen wir einmal für die Werte d = 2,3 mm, U = 300 V und A =
0,08009 m nach (2.Messreihe). Es
ergibt sich mit der aus der Theorie gewonnen Formel
Wie man erkennt,
ist der berechnete Wert in etwa doppelt so groß wie der gemessenen Wert von F = 6,08 mN. In der
Formel fehlt offensichtlich noch der Faktor „½“. Welchen
Fehler haben wir bei der theoretischen Herleitung gemacht? Wir
haben nicht beachtet, dass das elektrische Feld E sich aus den elektrischen
Feldstärken beider Platten zusammensetzt. Jede Platte erzeugt
aufgrund seiner Ladung ein eigenes E-feld E1 bzw. E2,
das sich zu
dem gesamten Feld E addiert. Es gilt also E = E1 + E2. Man
darf
also bei der Herleitung nicht das Gesamtfeld E wählen, sondern nur die
Hälfte davon, weil sich die untere Platte im Feld Eoben
= ½ E der oberen
Platte befindet. Für die
Formel zur Berechnung der Kraft auf eine Kondensatorplatte gilt
somit:
- zum Experiment - zu den
Messwerten und der Auswertung - zur Formel aus der
Auswertung - Formel aus der Theorie - zum
Kapitel „Coulombsches Gesetz“ -
zum Kapitel „Plattenkondensator“ |