|
zur Übungsaufgaben Übungsaufgabe
Nr.1 (mittel) Hinweis:
Um diese Übungsaufgabe zu bearbeiten, ist es notwendig sich mit dem Kapitel über die
Videoanalyse zu beschäftigen. Es soll folgende Bewegung einer
Luftkissenscheibe analysiert werden. Laden Sie das
Videoanalyseprogramm „Vimps“
und das Video
in den gleichen Ordner und halten Sie
sich an die Anweisungen im Kapitel Hier einmal kurz das Video (hier in hoher Qualität) zum Anschauen. Achten Sie besonders auf die Kalibierungsanzeige
und merken Sie sich die Länge des schwarzen Pfeils auf gelbem Grund. Werten Sie so lange aus, bis Sie die Bewegungsgleichung
für die Be- wegung angeben können. Lösung: Eine Analyse mit „vimps“
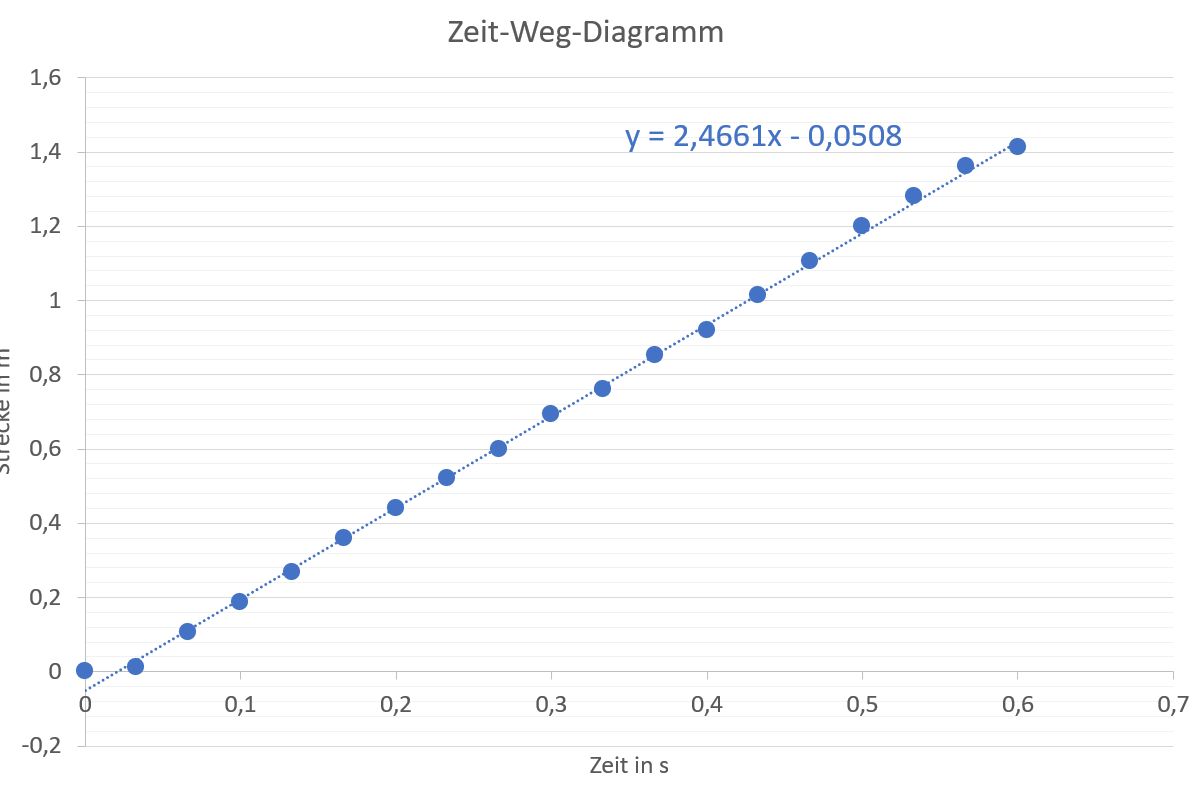
ergibt folgende Excel-Tabelle und -Dia- gramm:
Da ein linearer Verlauf im
Diagramm zu erkennen ist, muss es sich um eine gleichförmige
Bewegung handeln. Die Geschwindigkeit entspricht der Steigung des
Graphen, also v ≈ 2,5 m/s. Die Bewegungsgleichung lautet also: s(t) =
2,5 m/s ∙ t Übungsaufgabe
Nr.2 (leicht) Im Film „Jagd
auf Roter Oktober“ werden zwischen dem U-Boot „Roter
Oktober“ und dem amerikanischen U-Boot „USS Dallas“ akustische
Signale ausgetauscht, sogenannt „Pings“. Man spricht von einem
aktiven Sonar. Dies kann man zur Ortung von U-Booten be- nutzen. So
können auch Torpedos mit solch einem Ortungssystem (Ultraschallbereich)
ausgerüstet sein. Die „Pings“ zur Ortung von großen
Gegenständen, z.B. U-Booten, können im hörbaren Bereich (ca. 15
kHz) liegen. Fledermäuse müssen hochfrequente Signale (um 100 kHz)
aussenden, weil sie kleine Gegenstände (Insekten) orten wollen (s. Kapitel: Brechung (in Arbeit)).
Daher arbeiten die Torpedos auch mit mittleren
Frequenzen (40 kHz), weil sie ein U-Boot treffen sollen. Jetzt zur
Aufgabenstellung: a.) Roter
Oktober sendet einen Ping aus. Der Ping kommt nach 1,85 s zurück zum
U-Boot. Wie weit entfernt befindet sich dann die USS Dallas? [ vSchall
(Salzwasser) = 1480 m/s] b.) Ein Wal
in einer Entfernung von 15 km hört auch das akustische Signal. Wie
lange brauchte das Signal, bis es den Wal erreichte? c.) Vor
einer Fledermaus befindet sich in einer Entfernung von 40 cm ein großes
Insekt. Die Fledermaus hört das Echo nach 2,4 ms.
Wie groß ist
die Schallgeschwindigkeit in der Luft? d.) Man
kann auch Lichtsignale zwischen U-Booten austauschen, wenn beide
aufgetaucht sind. Zwei U-Boote haben einen Abstand von 300 m und
morsen mit Lichtsignalen. Wann kommt das Lichtsignal beim
anderen U-Boot an. (vLicht(Luft) = 299 710 km/s) e.)
Entsteht bei einem Gewitter ein Blitz wird sowohl ein Lichtsignal als auch ein
akustisches Signal (Donner) abgesandt. Ein Beobachter befindet
sich 5 km entfernt vom Ort der Blitzentstehung. Wie groß ist die
Zeitdifferenz zwischen optischem und akustischem Signal beim Beobachter? Lösung: Es liegt in allen Fällen eine gleichförmige Bewegung vor. zu a.) gegeben: v = 1480 m/s; t = 1,85 s gesucht: d = Abstand des U-Bootes
zu b.) gegeben: s = 15 km = 15 000 m; v = 1480 m/s gesucht: t
zu c.) gegeben: s = d
= 40 cm = 0,4 m; t = 2,4 ms = 0,0024 s gesucht:
v
zu d.) gegeben: s =
300 m; v = 299 710 km/s gesucht:
t
zu e.) gegeben: s = 5
km = 5000 m; vLicht = 299 710 km/s; vSchall
= 333,3 m/s gesucht:
∆t = tSchall − tLicht
Die Zeit für das
Licht spielt keine Rolle. Die Zeitdifferenz wird durch die Zeit für den
Schall bestimmt. Es gilt die 3-Sekunden Regel: Man zählt die Zeit zwischen Blitz
und Donner und teilt
diese Zeit durch 3, dann erhält man die Entfernung des Gewitters. Übungsaufgabe Nr.3 (schwer) Ein PKW mit Anhänger und ein LKW fahren auf der Autobahn mit jeweils einer Geschwindigkeit von 80 km/h. Der PKW mit Anhänger hat eine Länge von 12 m. Der LKW ist 18 m lang. Der Abstand zwischen PKW und LKW beträgt 40 m (nach der Halbe-Tacho-Regel). Der PKW entschließt sich den LKW mit einer Geschwindigkeit von 100 km/h zu überholen und schert dann 30 m vor dem LKW wieder ein. a.) Wie lange braucht der
PKW mit Anhänger für den Überholvorgang? Welche Strecke hat dann der PKW
zurückgelegt? b.)
Zwei LKWs führen auf der Autobahn ein verbotenes „Elefanten- rennen“
durch. Der LKW A überholt mit 85 km/h einen LKW B mit einer
Geschwindigkeit von 80 km pro Stunde. Es sollen die Mindest- abstände
von jeweils 50 m eingehalten werden. Die LKWs sind jeweils 18 m
lang. Welche
Werte ergeben sich in diesem Fall für die Zeit und die Strecke? Hinweis: Der Beschleunigungsvorgang und das Ein- und
Ausscheren werden nicht berücksichtigt. Es wird von einer
gleichförmigen Bewe- gung ausgegangen. Lösung: zu a.) gegeben: vPKW = 100 km/h; vLKW = 80 km/h; verschiedene Strecken: sPKW = 12 m, sLKW = 18 m; dPKW-LKW = 40 m; dLKW-PKW = 30 m gesucht: t = Zeit für den Überholvorgang, s = zurückgelegte PKW- Strecke Da der Beschleunigungsvorgang und das Aus- und Einscheren unbe- rücksichtigt bleibt, kann man auch so tun, als ob sich der PKW schon bei 40 m Abstand vom LKW auf der Überholspur befindet und ab hier ohne Zeitverzögerung auf 100 km/h beschleunigt. Der PKW muss dann (man wähle z. B. die vordere Stoßstange) 100 m für den Überholvorgang zurücklegen ( 40 m + 18 m + 30 m + 12 m). 1. Möglichkeit der Rechnung: Man betrachtet nur die Geschwindigkeitsdifferenz zwischen LKW und PKW und legt hiermit die 100 m zurück, d.h. man tut so, als ob der LKW stehen würde. Es gilt dann:
2. Möglichkeit: t = Zeit für den
Überholvorgang Ansatz: ∆ s = sPKW − sLKW
= 100 m → vPKW ∙ t − vLKW ∙ t = 100 m nach t umgestellt,
führt zum selben Ergebnis b.) gegeben: vA = 85 km/h; vB
= 80 km/h s = 50 m + 50 m + 18 m
+ 18 m = 136 m
Es liegt in diesem
Fall ein nicht erlaubtes „Elefantenrennen“ vor. Nach dem Strafrecht
soll ein Überholvorgang nach 45 s abgeschlossen sein. Dafür müssten
die LKWs aber mindestens eine Geschwindigkeits- differenz
von 10 km/h aufweisen. Wenn man es einmal nachrechnet, kommt man bei ∆v
= 10 km/h auf t = 49 s, was eigentlich auch noch zu hoch ist. Wenn die
LKWs also die Höchstgeschwindigkeit einhalten wollen und im
rechtlichen Rahmen bleiben möchten, müsste der LKW, der überholt wird,
die Geschwindigkeit auf 70 km/h reduzieren. Mit anderen Worten: Das Überholen eines LKWs durch einen LKW ist normalerweise im rechtlichen Rahmen nicht möglich!!! Extra: Link-Liste zum Thema
Übungsaufgabe Nr.4 (mittel) Ein Radfahrer fährt mit einer konstanten
Geschwindigkeit von 4 m/s (14,4 km/h) eine ebene Straße entlang. Am Punkt B
beginnt man mit der Zeitmessung (t = 0 s). Der Radfahrer hat dann aber
ab dem Punkt A schon eine Strecke von 10 m zurückgelegt. Man
will jetzt die Strecke von A aus gegen die Zeit t auftragen. a.) Zeichen Sie das Zeit-Weg−Diagramm. b.) Geben Sie die Bewegungsgleichung (s in Abhängigkeit
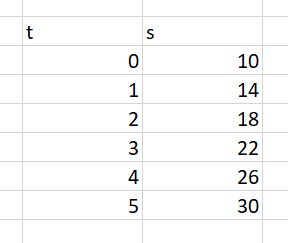
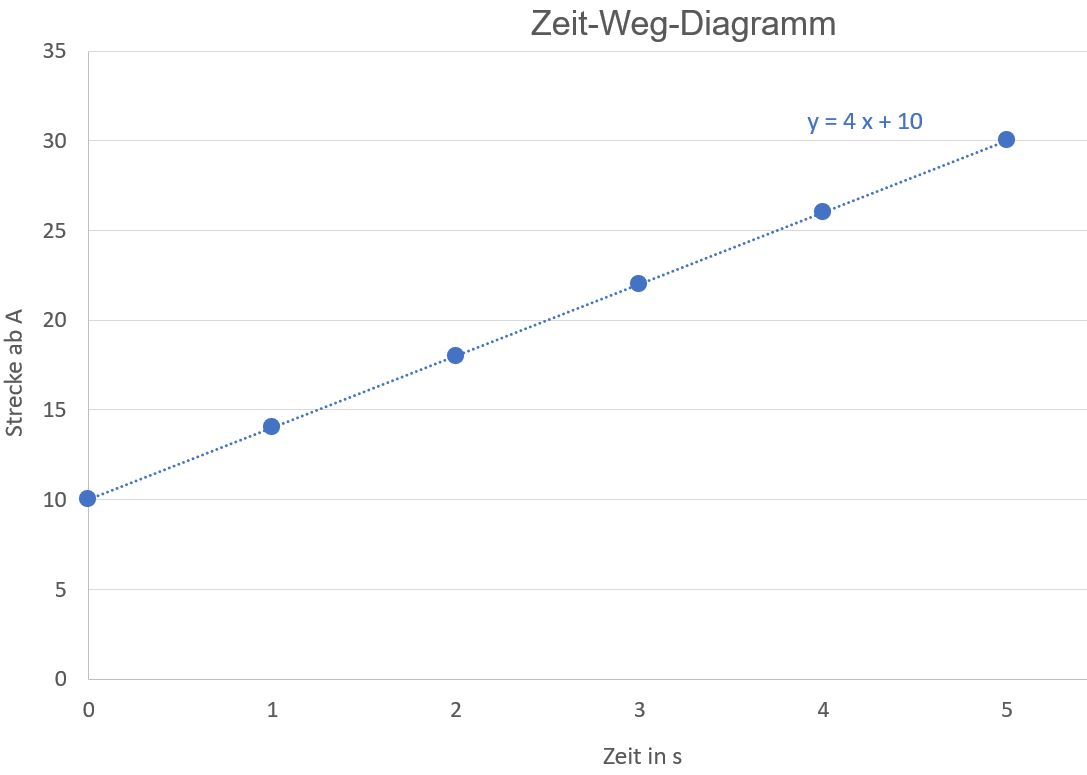
von t) für diesen Fall an. Lösung: a.) Man erhält z.B. folgende Excel-Auswertung
b.) Es ergibt sich (s.Trendlinie): s(t) = 4 m/s ∙ t + 10 m Im allgemeinen Fall (t = 0 s nach einem zurückgelegten Weg s0 und einer Geschwindigkeit v) gilt. s(t) = v ∙ t + s0 zurück zu zum vorherigen Kapitel zum nächsten Kapitel |