|
1.
Aufgabe a.) Skizzieren Sie den
Feldlinienverlauf (mit Richtungsangabe) des elektrischen Feldes - in einem geladenen
Plattenkondensator - in der Umgebung einer positiv
geladenen Kugel b.) Geben Sie Unterschiede zwischen den beiden Feldern an. c.) Man gibt jeweils eine
negative Probeladung in die beiden Felder. Geben Sie an, wie sich diese
Ladung in den jeweiligen Feldern (Bewegungsform, Kräfte,
Beschleunigungen) verhält. Lösung:
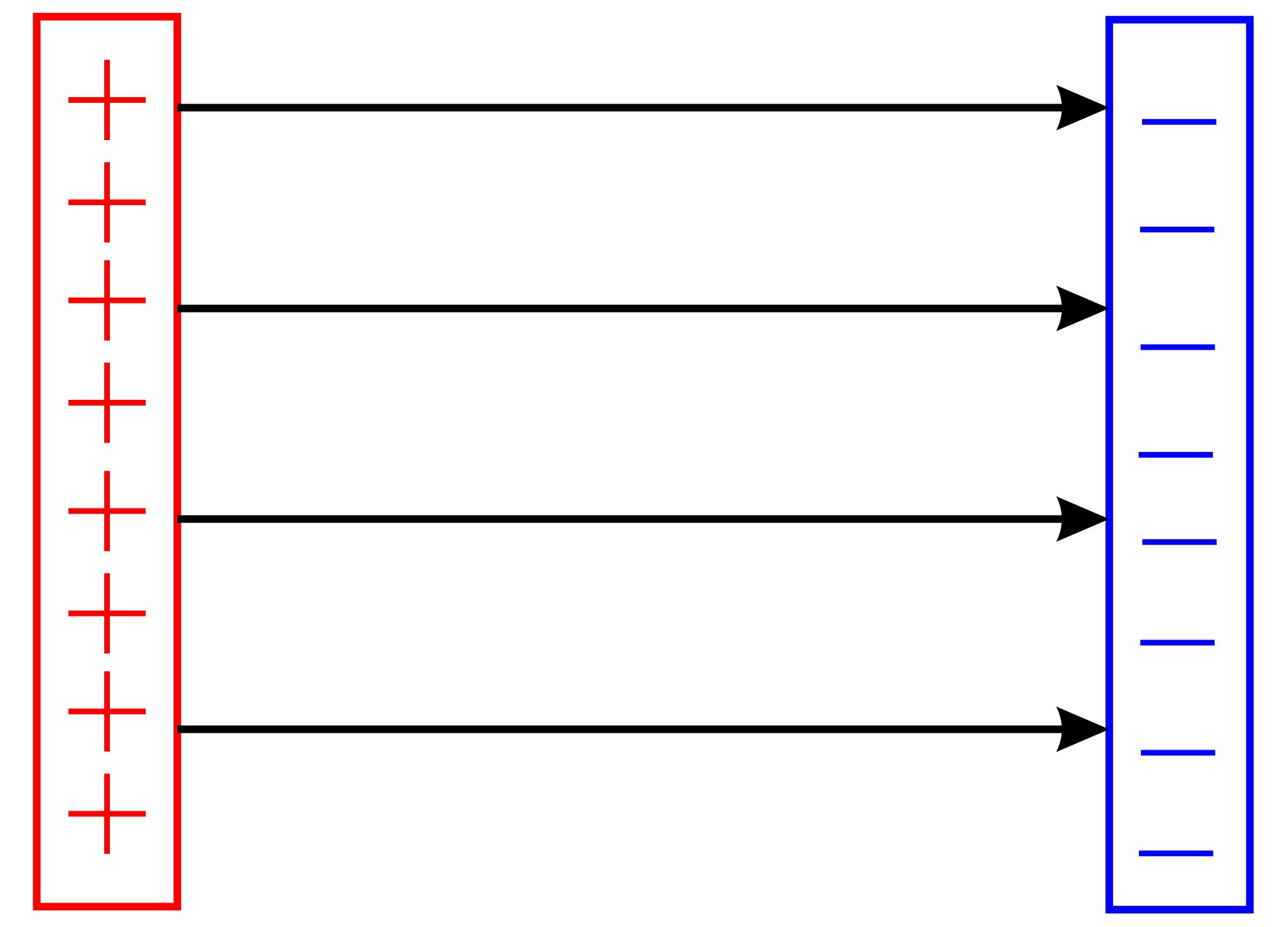
b.) Plattenkondensator: homogen, alle Feldlinien parallel im gleichen
Abstand; senkrecht auf den Platten; Richtung von der Plus−Platte
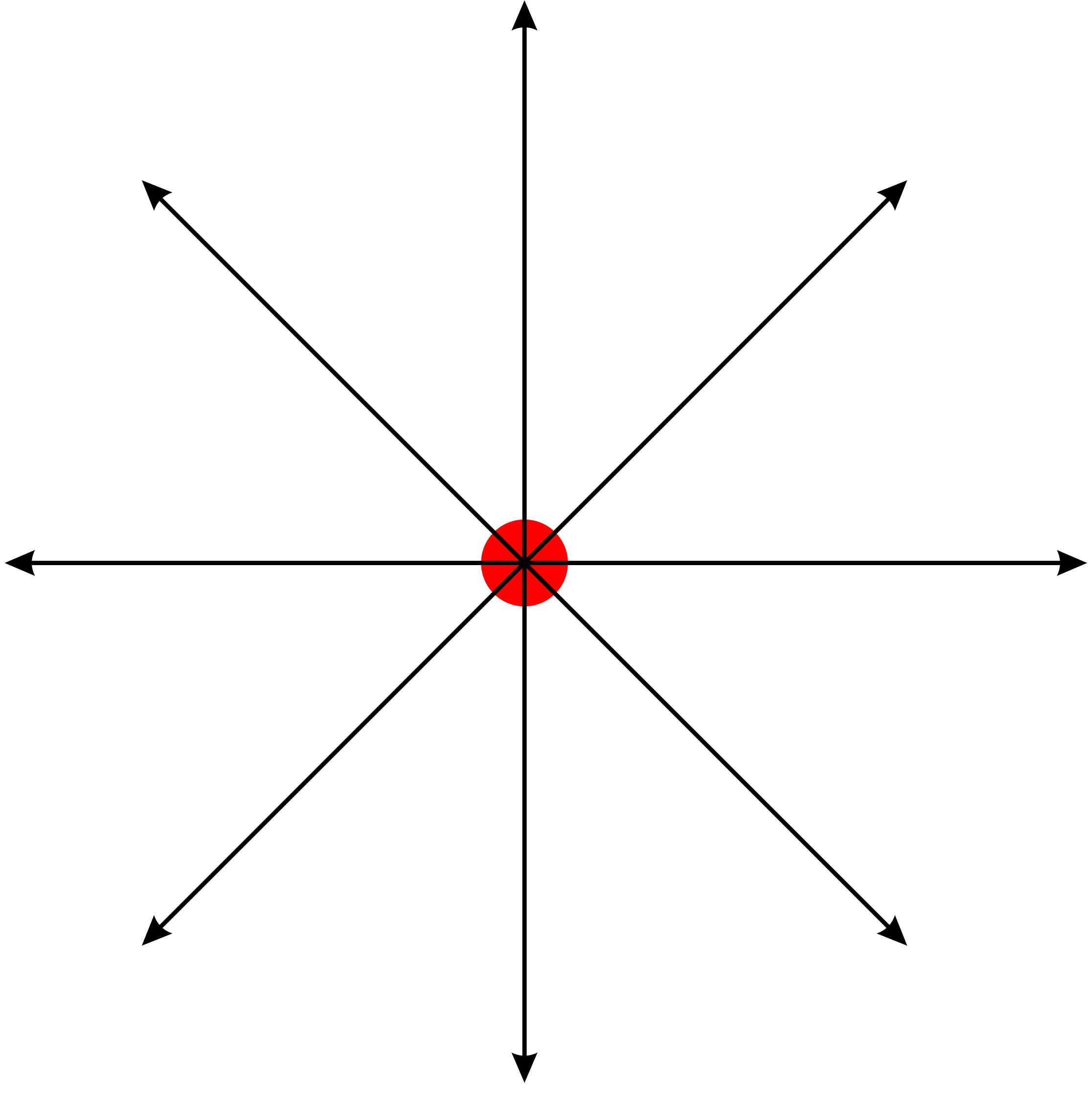
zur Minus−Platte geladene positive Kugel: radialsymmetrisches Feld, Richtung von der
Kugel weg, Feldlinien senkrecht auf der Kugeloberfläche, in der Nähe
der Kugel dichter als weiter weg c.) Plattenkondensator: konstante Kraft, gleichmäßig beschleunigte
Bewegung, d.h. Beschleu- nigung konstant, v nimmt linear mit t zu (v=a∙t); negative Ladung be- wegt sich mit konstanter Beschleunigung auf die
positive Platte zu geladene positive Kugel: Feld nicht homogen; Kräfte sind nicht konstant;
Kraft in der Nähe größer als weiter weg; Beschleunigung nicht
konstant, sondern wird immer größer je näher man der Kugel kommt;
Geschwindigkeit nimmt schneller als linear zu; die negative Ladung
bewegt sich auf die Kugel mit immer größerer Beschleunigung mit stark
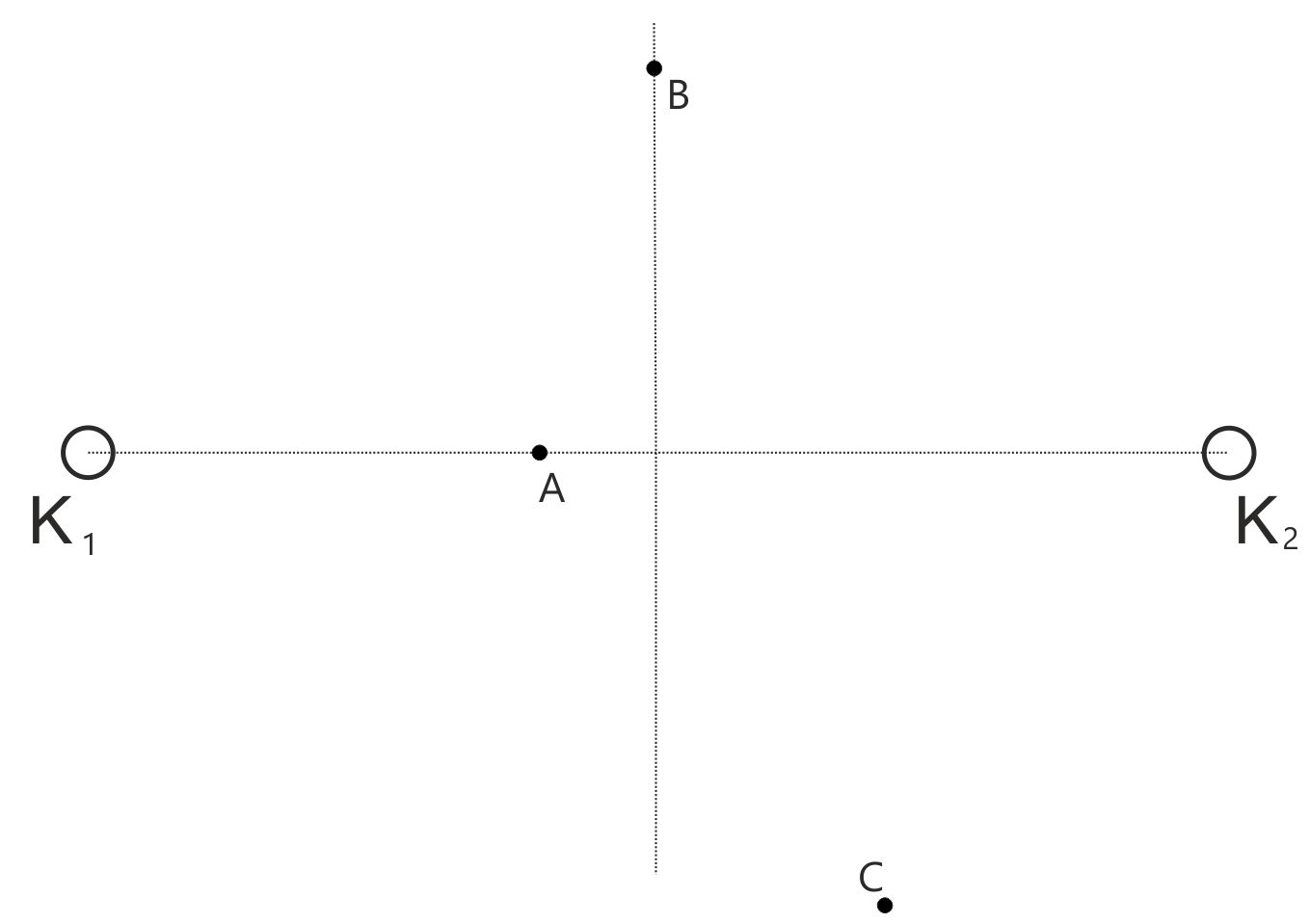
zunehmender Geschwin- digkeit zu. 2. Aufgabe Die offenen Kreise stellen
positiv geladene Kugel dar. Die Ladung ist gleich groß. In den schwarzen
Punkten soll die elektrische Feldstärke konstruiert werden. Für die
elektrische Feldstärke einer Kugel in Ab- hängigkeit vom Abstand gilt
: E(x) = 3,6 V∙m
/ x2 ( x = Abstand in
Metern vom Kugelmittelpunkt) a.) Bestimmen Sie zunächst den
Betrag der Feldstärke von den ein- zelnen Kugeln K1 bzw. K2
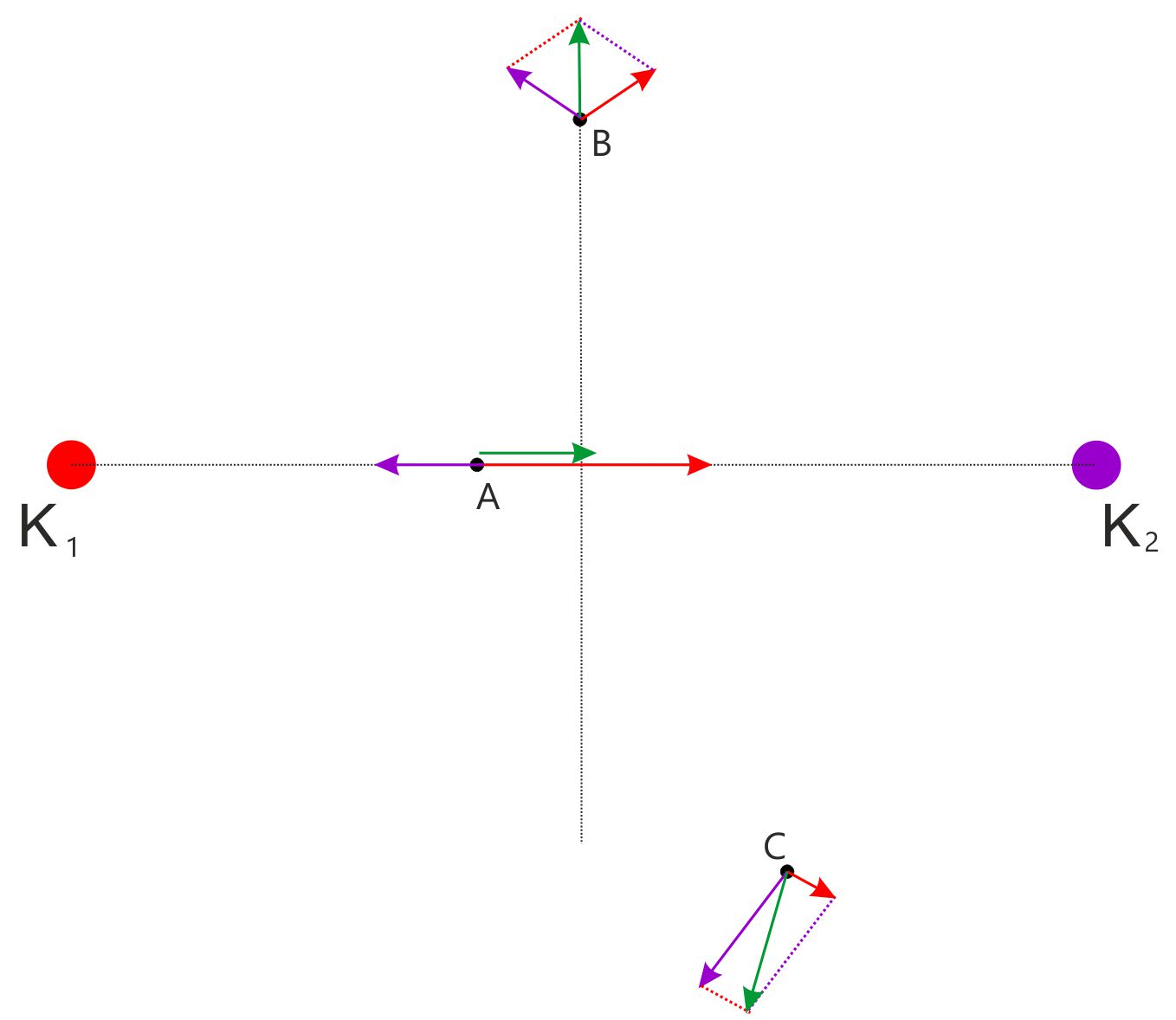
in den markierten Punkten A, B und C. (Abstände auf volle Zentimeter runden) b.) Konstruieren Sie danach die
Gesamtfeldstärke in den Punkten A, B und C. [Hilfslinien
gestrichelt zeichnen, die Gesamtfeldstärke mit einem durchgezogenen Pfeil
eintragen. ( Einheit: 1 cm ≡ 1000 V/m)]
Lösung: Punkt A: 4 cm von K1 und 6 cm von K2
entfernt E1(A) = 2250 V/m; E2(A)
= 1000 V/m; EG(A) = 2250 V/m −
1000 V/m = 1250 V/m (Richtung K2) Punkt B: 6 cm von beiden
Kugeln E1(B) = E2(B)
= 1000 V/m; EG(B) mit „Kräfteparallelogramm“ Punkt C: 8 cm von K1
und 5 cm von K2 E1(C) = 562,5 V/m;
E2(C) = 1440 V/m; EG(C) mit „Kräfteparallelogramm“
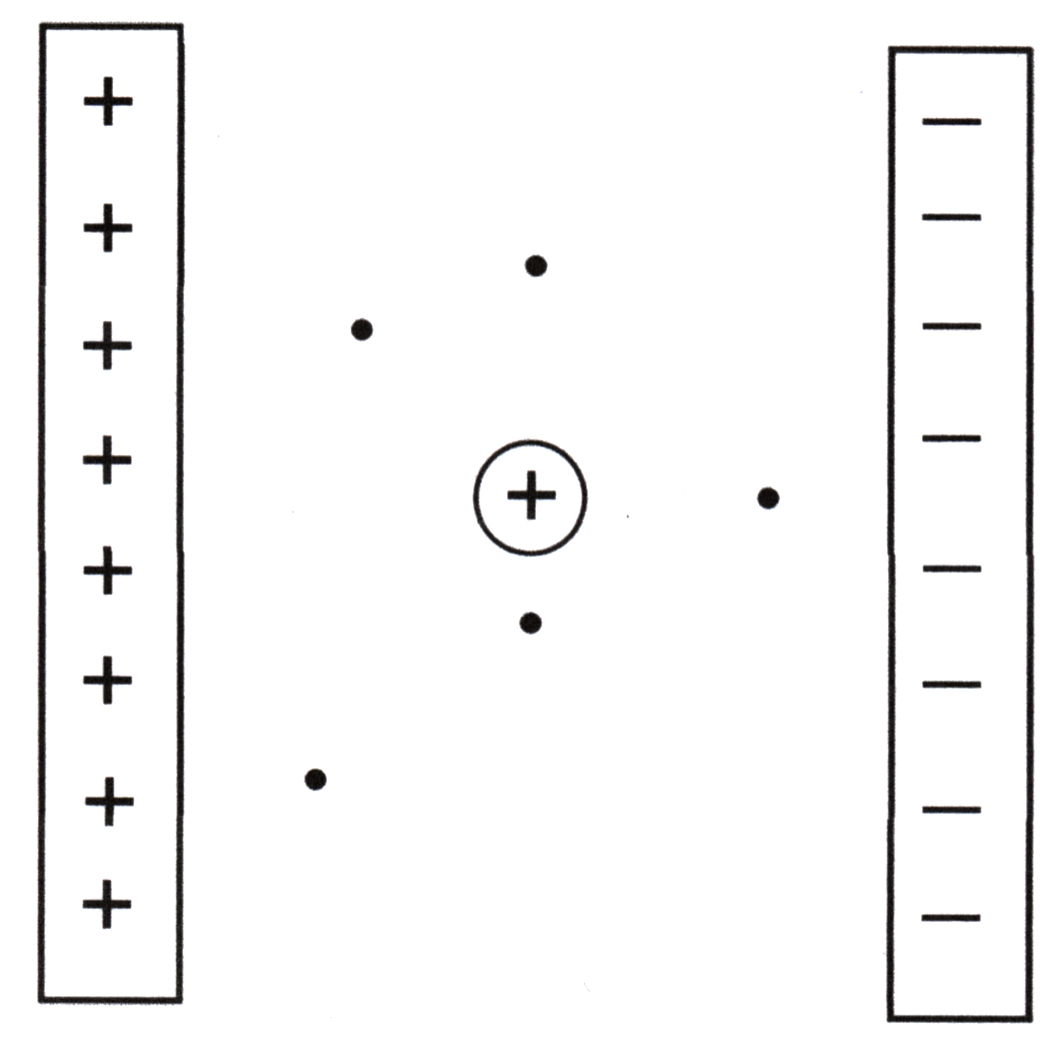
3. Aufgabe Konstruieren Sie den
Feldstärkeverlauf (Angabe mit Betrag und Richtung) in den vorgegebenen Punkten der
Abbildung (Wähle 1 cm º 10 kV/m). Die elektrische Feldstärke soll im
Plattenkondensator 10 kV/m betragen. Die Kugel erzeugt in einem
Abstand von 1 cm vom Kugelmittelpunkt eine Feldstärke von 36 kV/m. Für
die elektrische Feldstärke einer Kugel gilt: E = C / r2 r = Entfernung
vom Kugelmittelpunkt in cm (C ist die Proportionalitätskonstante). Hinweis:
Bestimmen Sie bei der Kugel zunächst die Konstante C. Die Entfernung der
Punkte von der Kugelmitte kann auf volle
„cm“ gerundet werden.
Lösung: Bestimmung von C: r = 1 cm → E = 36
kV/m mit C = E ∙ r2
= 36 000 V/m ∙ (0,01 m)2 = 3,6 V∙m für alle Punkte mit r = 2 cm
gilt: EK = 3,6 V∙m∙1/(0,02m)2 = 9000 V/m für den Punkt mit r = 3 cm
gilt: EK = 3,6 V∙m∙1/(0,03m)2 = 4000 V/m Das homogene Feld verläuft
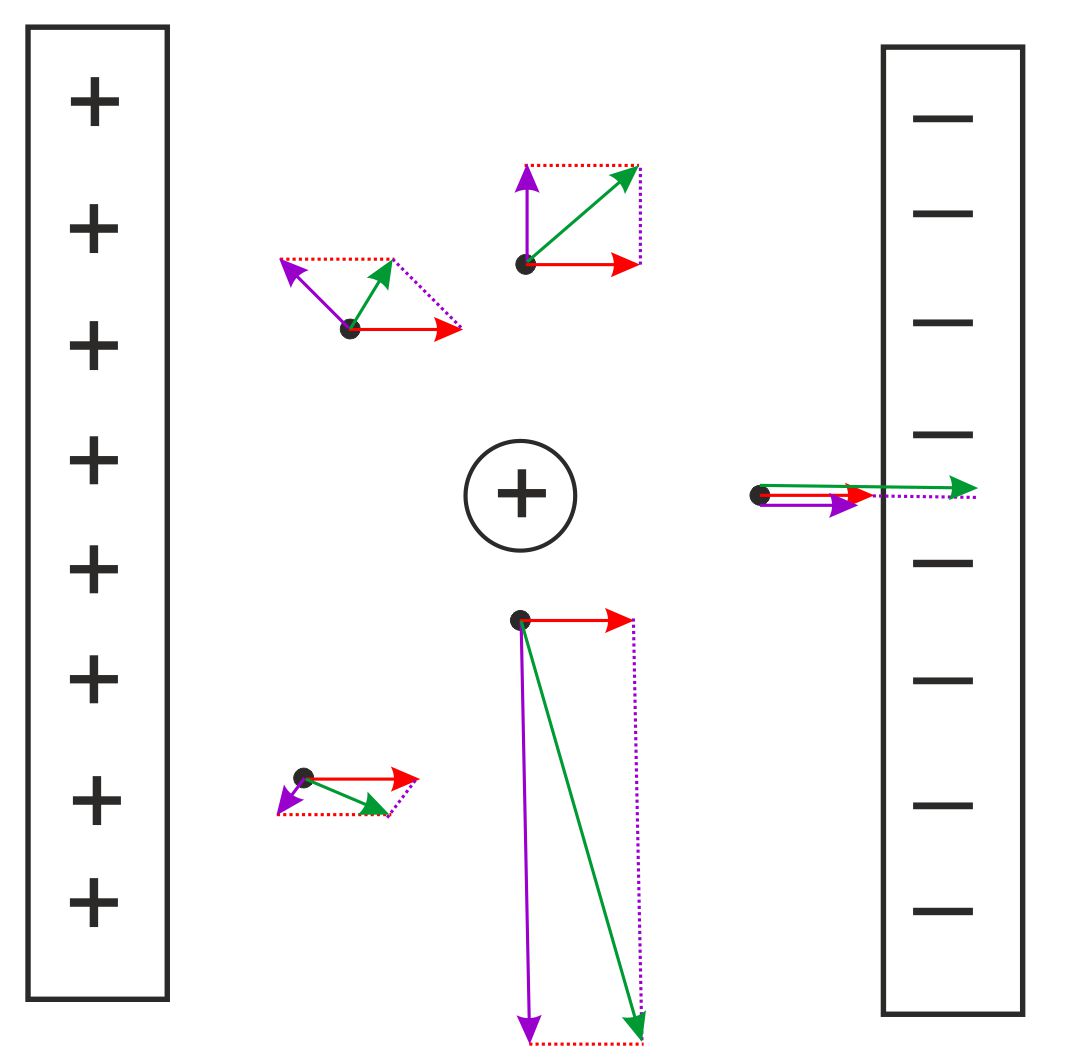
senkrecht zur positiven Platte an jeder Stelle mit E = 10 kV/m (º 1 cm) (roter Pfeil) Das Feld der Kugel verläuft radial zur Kugel
(violetter Pfeil) Die Gesamtfeldstärke (grüner
Pfeil) ergibt sich durch Vektoraddition.
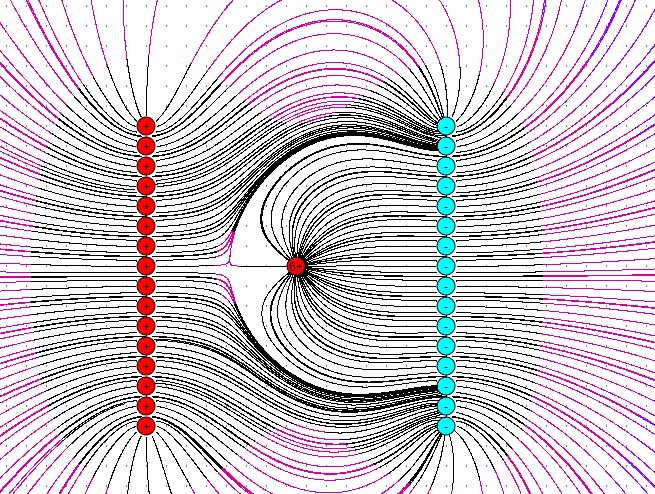
Im Folgenden
sehen Sie das entsprechende Feldlinienbild mit dem Programm von Girwidz gezeichnet.
-
zu Aufgabe Nr.1 - zu Aufgabe Nr.2 - zu Aufgabe Nr.3 - zum Kapitel
„Plattenkondensator-Linkliste“ |