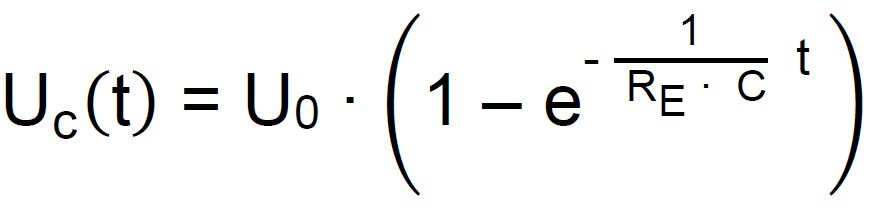Abituraufgaben

Aufgabe Nr.1 (LK)

Vorgegeben ist ein Kondensator der Kapazität C, eine Spannungs-

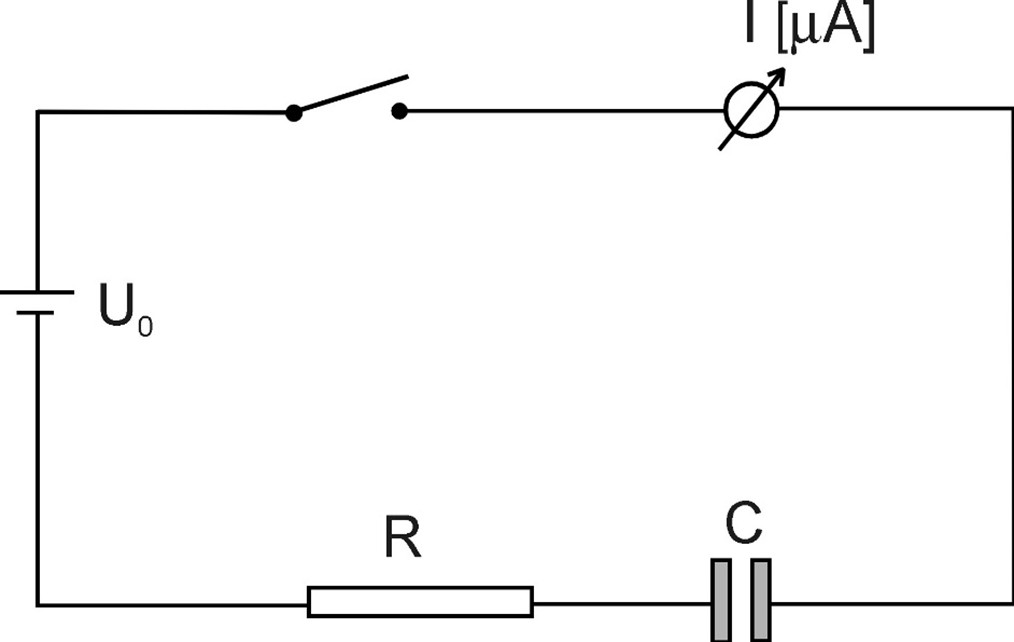
quelle U₀ und ein ohmscher Widerstand R. Die Bauelemente sind ent-

sprechend der Schaltskizze verbunden. Das Messgerät weist den

Innenwiderstand R_i auf.

a.) Der Schalter wird geschlossen (t = 0 s). Der zeitliche Verlauf der

Stromstärke wird nun gemessen. Die Tabelle zeigt eine solche Mess-

reihe.

I in μA	65	45	34	25	18	13	9	7	5	4	3	1
t in s	0	2	4	6	8	10	12	14	16	18	20	25

In diesem Fall galten folgende Werte:

U₀ = 40 V, C = 10 μF, R_i= 120 kΩ, R = 500 kΩ

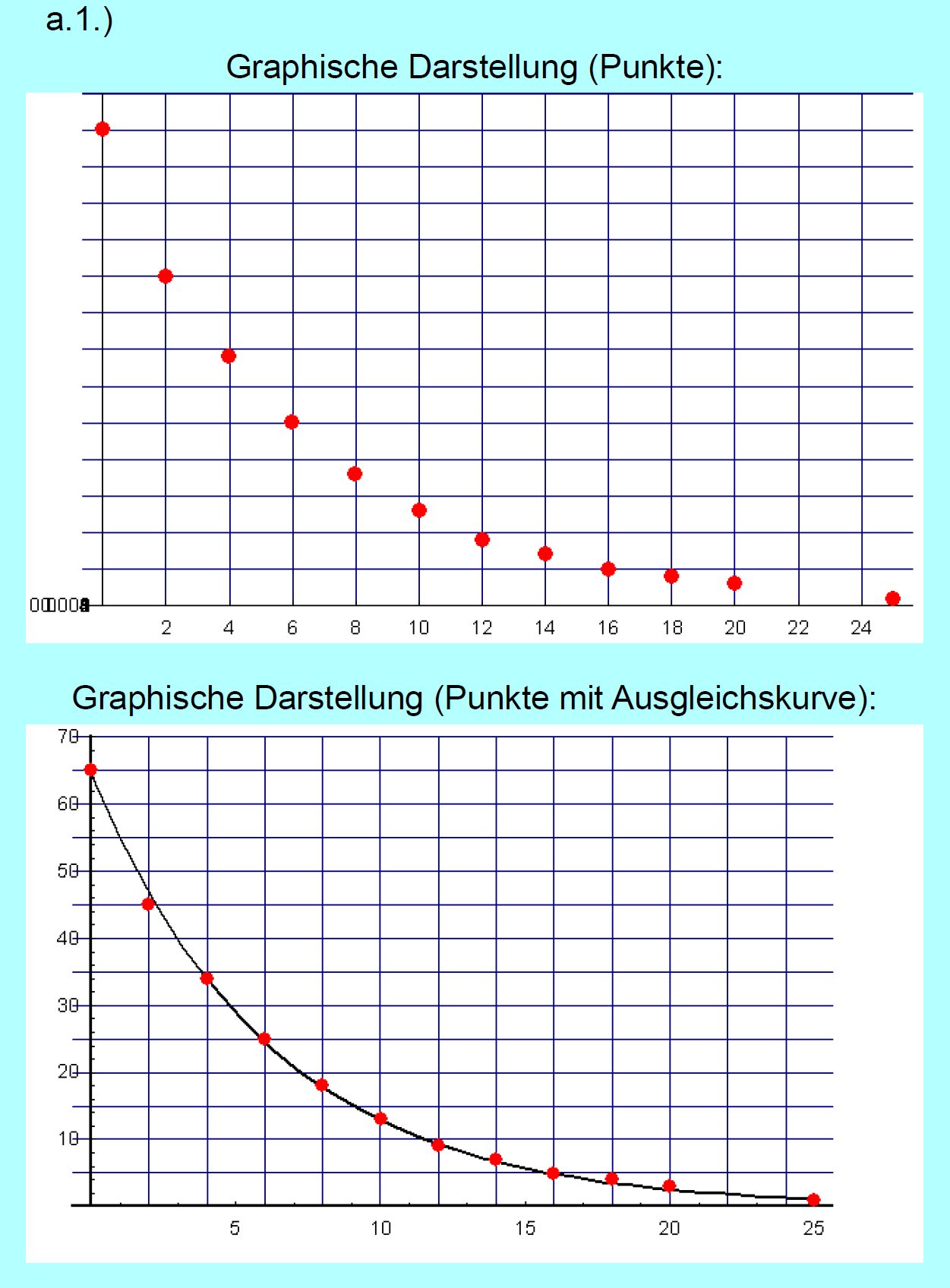
1.) Stellen Sie die Messwerte graphisch dar [ x-Achse: t, y‑Achse: I ( t ) ].

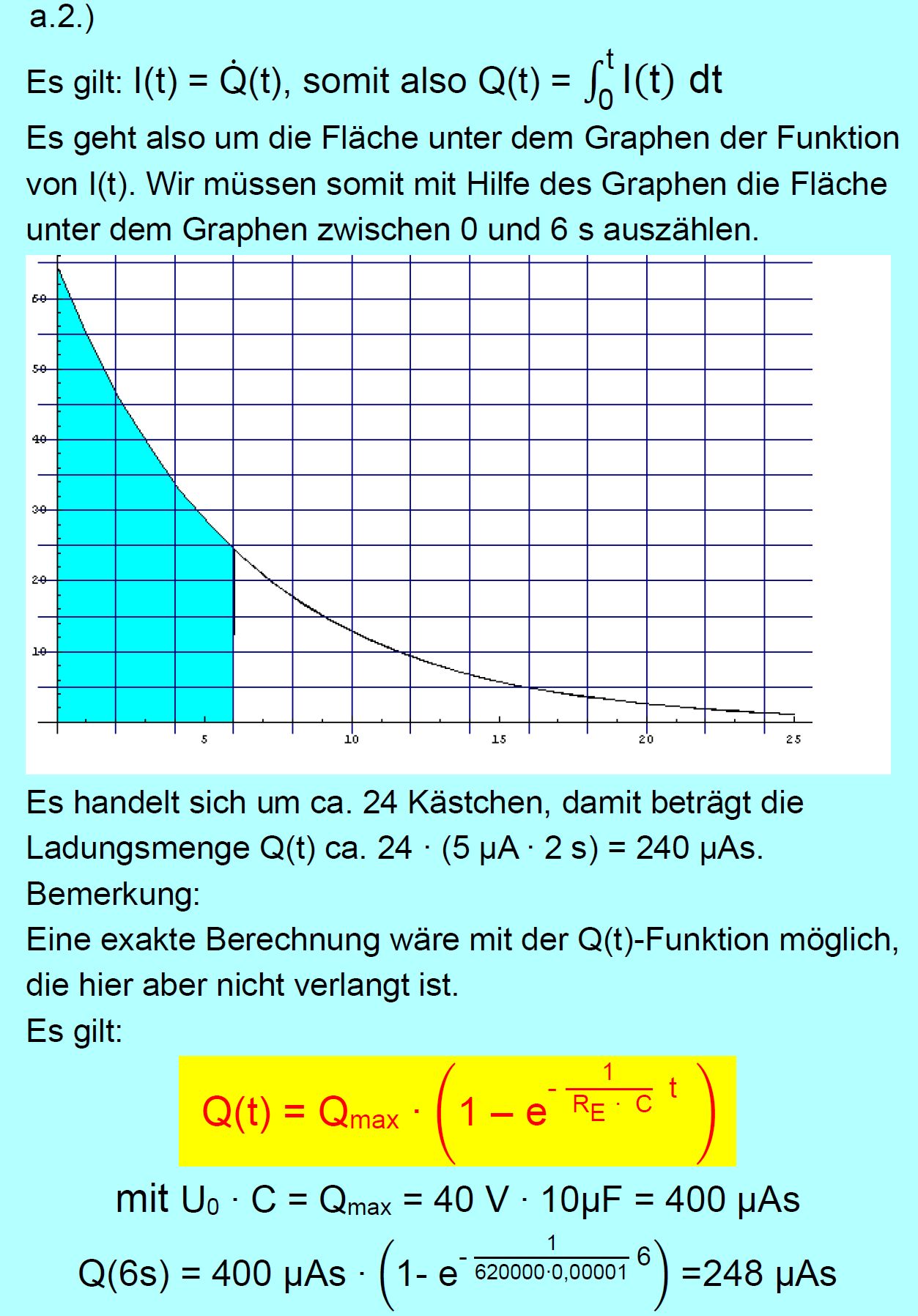
2.) Erklären Sie, wie man aus dem Stromstärke-Zeit-Diagramm die

Ladungsmenge bestimmen kann, die im Stromkreis bis zu einem Zeit-

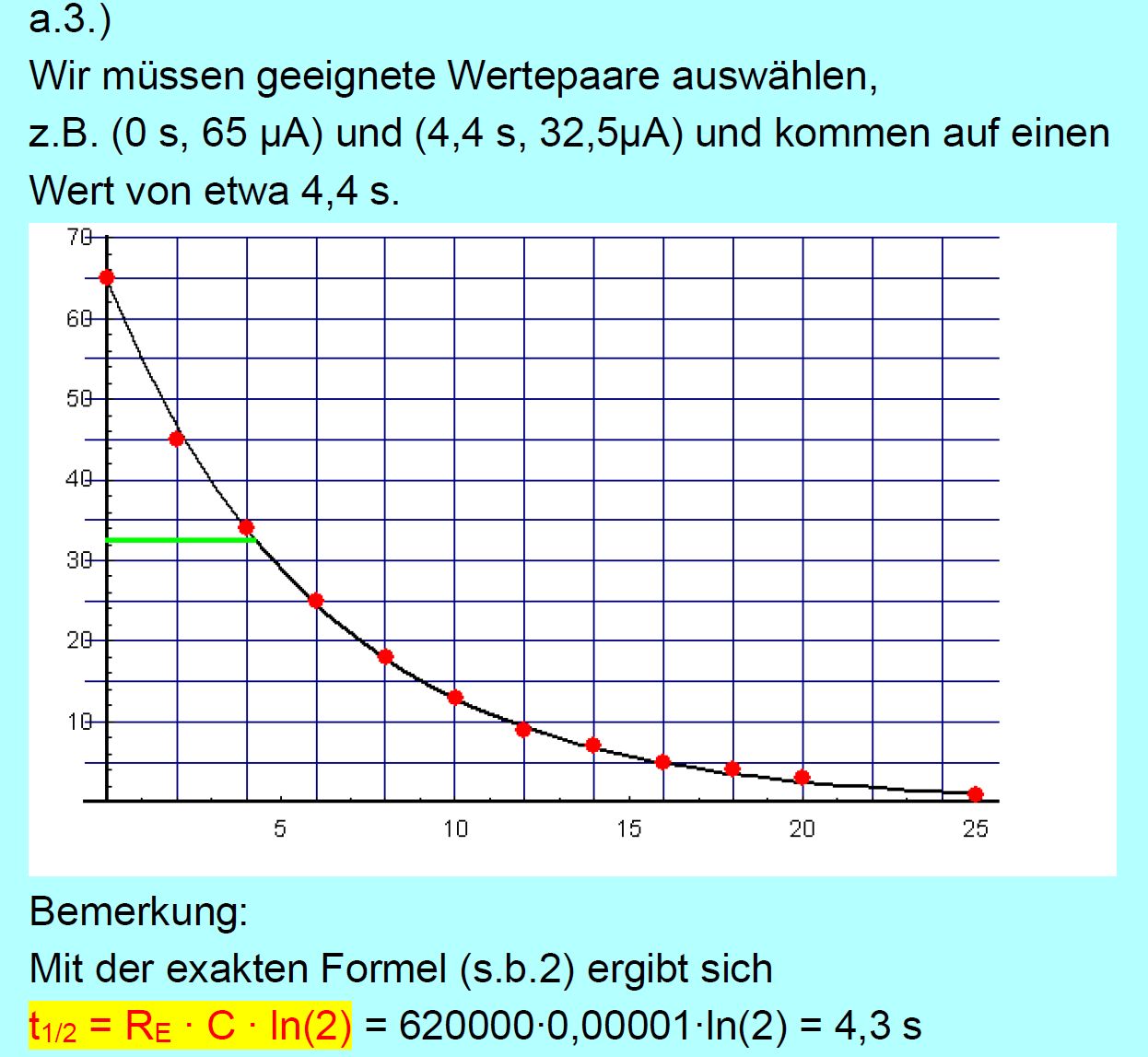
punkt t geflossen ist. Bestimmen Sie die geflossene Ladungsmenge

bis zum Zeitpunkt t = 6 s.

3.) Welche Halbwertszeit lässt sich aus dem Diagramm entnehmen?

b.1.) Leiten Sie einen Funktionsterm für I ( t ) her (allgemeiner Fall).

Hilfe: Benutzen Sie den Ansatz U₀ = U ( t ) + U_C( t ) mit

Es gilt außerdem:

U ( t ) = Spannung am gesamten ohmschen Widerstand R_E; R_E = R + R_i

U_C( t ) = Spannung am Kondensator

Zur Kontrolle:

2.) Leiten Sie aus I ( t ) eine Gleichung für die Halbwertszeit her.

Kontrollieren Sie hiermit Ihr Ergebnis aus a.)3.).

c.) Für die Spannung am Kondensator gilt für das Aufladen (Gleich-

stromfall).

Es gelte: U₀ = 12 V, R_g = 1,2 MΩ, C = 40 μF

1.) Bestimmen Sie U( t ) nach 10 s und nach 250 s.

2.) Nach welcher Zeit gilt U_C( t ) = 99% von U₀? Stellen Sie zunächst

eine Formel zur Berechnung auf und setzen Sie danach die konkreten

Werte ein.

Lösung:

b.1)

c.)

Formel nachsehen.

zurück zum Kapitel: