|
Überlagerung von Schwingungen -
Interferenz Da es in diesem Kapitel um Schwingungen geht,
sollte man sich vorher auf jeden Fall mit Schwingungen beschäftigt haben und hier
insbesondere mit den harmonischen
Schwingungen. Am Anfang unserer Betrachtungen steht, wie so
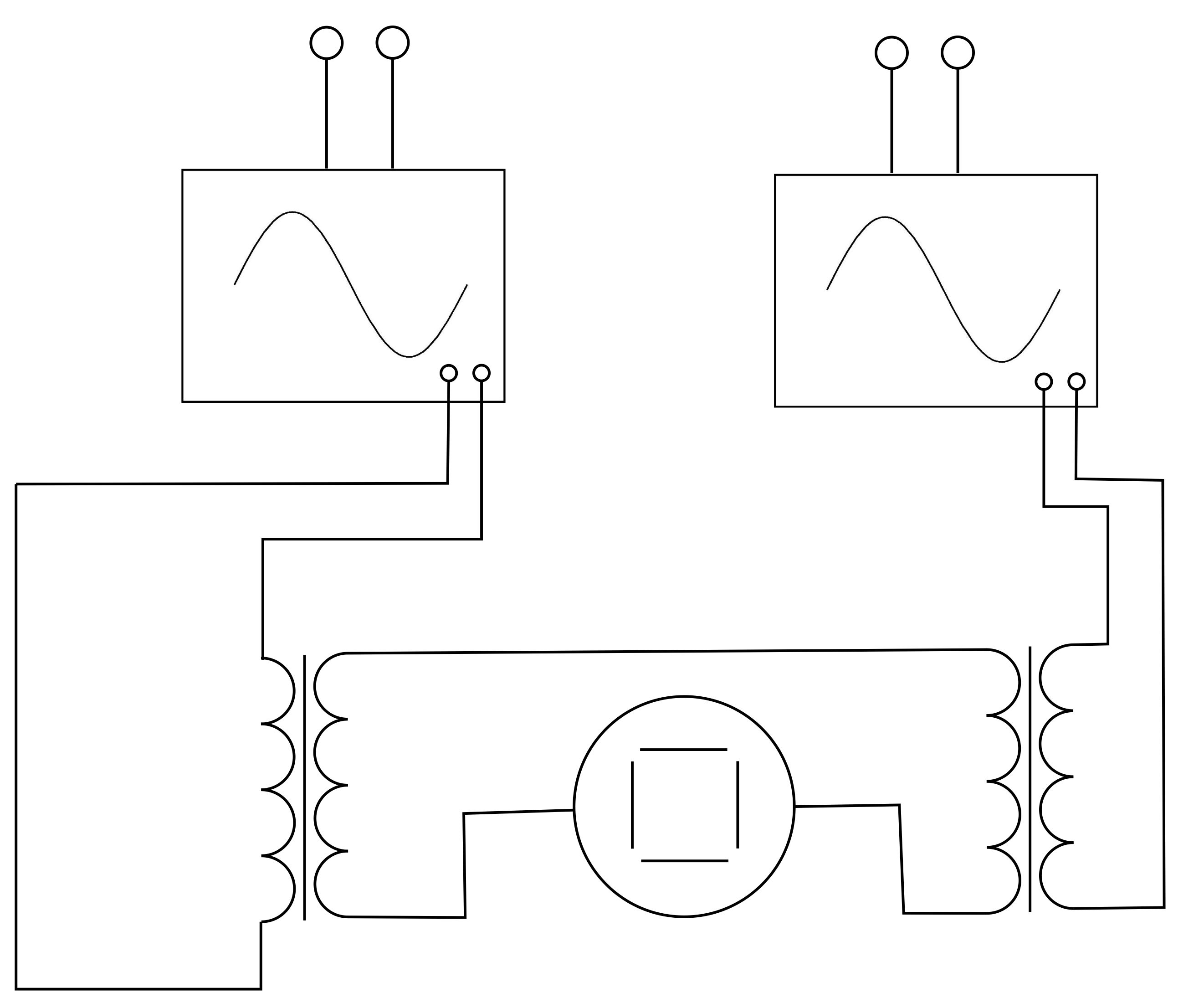
häufig, ein Versuch. 1. Versuchsaufbau: Überlagerung elektrischer
Schwingungen
Der Versuchsaufbau besteht aus zwei
Sinusgeneratoren, die elektrische Sinus-schwingungen erzeugen. Bei diesen
Schwingungen können unterschiedliche Frequenzen eingestellt werden. Diese
Schwingungen werden jeweils der Primärseite eines Transformators zugeführt.
Die Schwingungen auf der Primärseite werden auf die Sekundärseite übertragen.
Beide Sekundärseiten sind miteinander verbunden, so dass hier die
Überlagerung der Schwingungen stattfindet, die dann auf einem Oszilloskop zu
sehen ist. Einfache Versuche: 1. Fall:
Beiden Seiten wird genau die gleiche Frequenz zugeführt. Dies geht
nur, indem man beide Transformatoren mit demselben Sinusgenerator verbindet.
Je nachdem, wie die Kabel am zweiten Transformator angeschlossen sind,
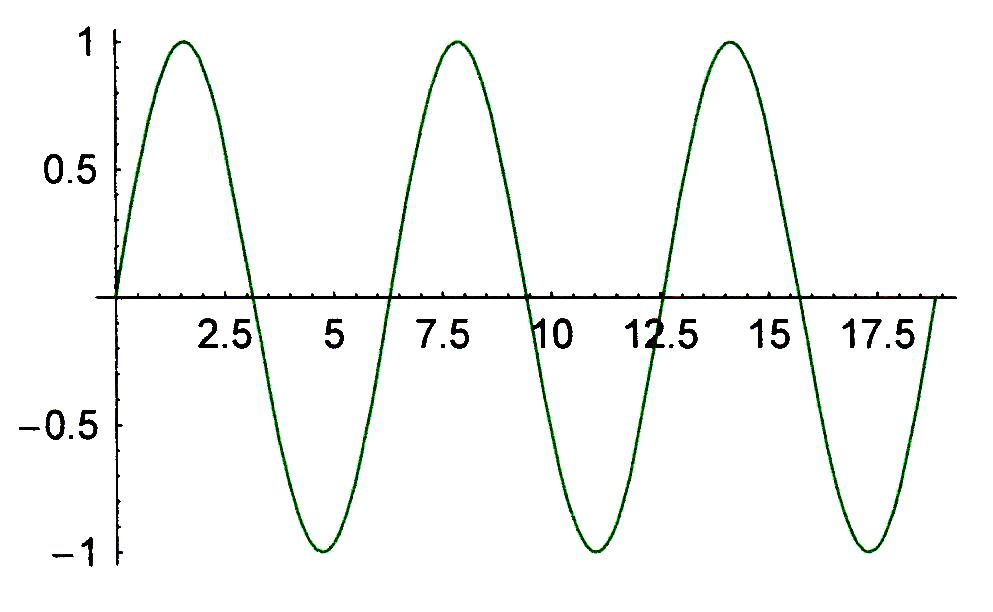
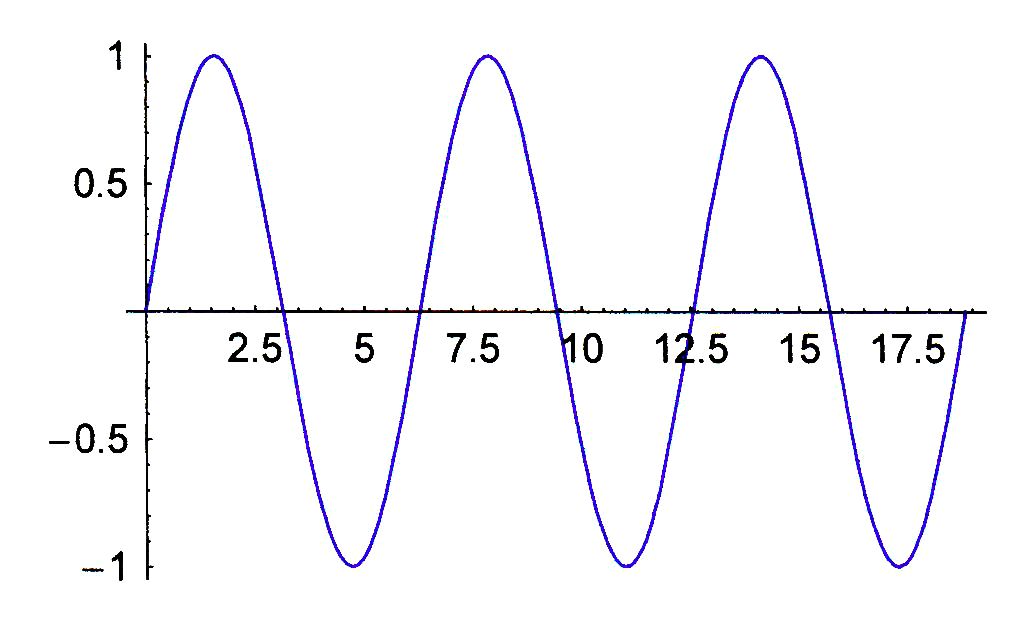
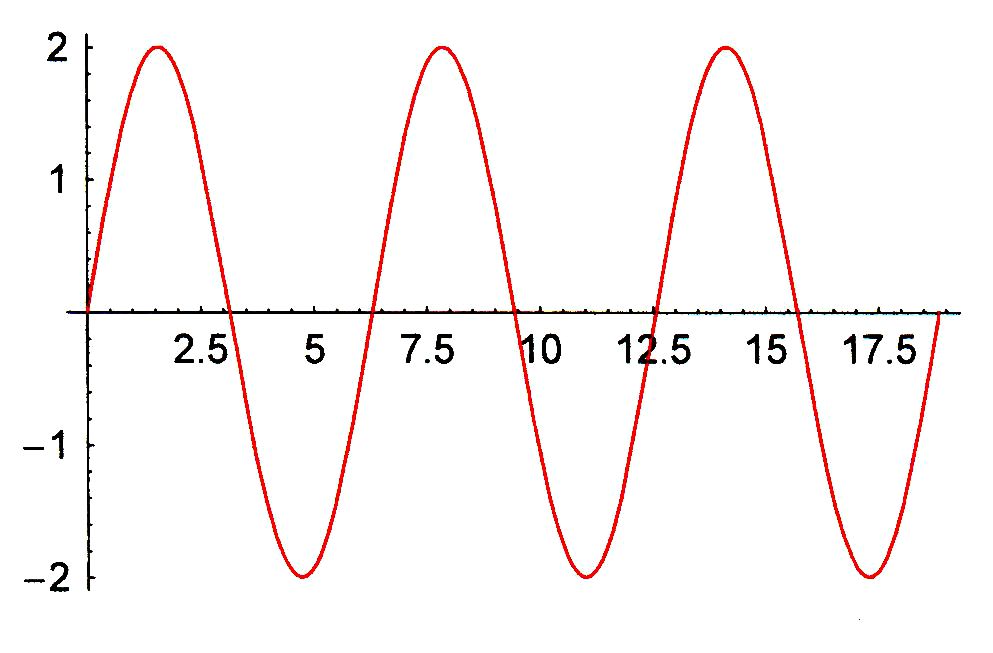
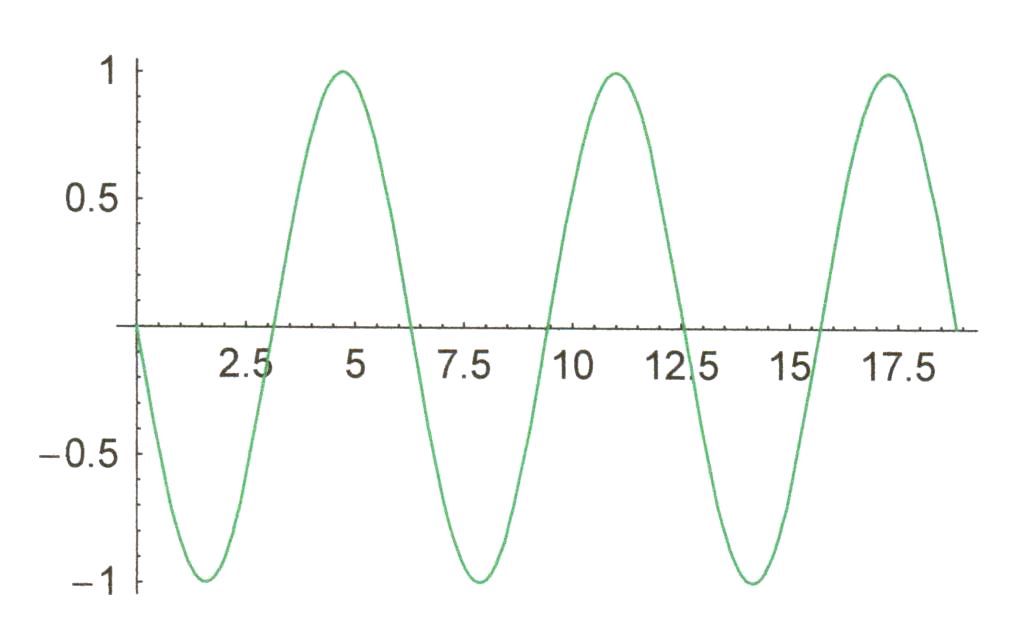
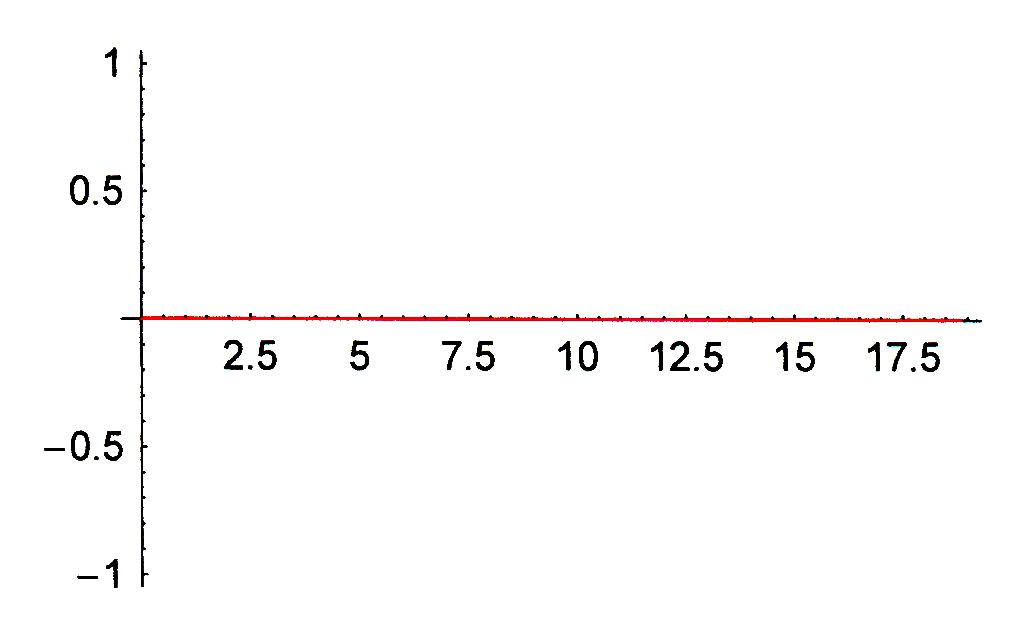
überlagern sich die Schwingungen gleichphasig oder gegenphasig. Beobachtung: Bei gleicher Phase verstärken
sich die Schwingungen. Die Frequenz bleibt gleich, die Amplitude ist doppelt
so groß. Bei einer gegenphasigen Überlagerung verschwindet die Schwingung. Graphisch sieht das folgendermaßen aus:
Interpretation: Man erkennt, dass sich die Ausschläge
(Elongationen) zu jedem Zeitpunkt addieren. Es liegt das Superpositionsprinzip vor,
welches wir schon aus der Mechanik bei komplexen Bewegungen kennen. Im
Bereich der Schwingungen kann man dies folgendermaßen formulieren.
2.Fall: Mit etwas Geschick kann man bei dem
Versuch auch noch Frequenzen einstellen, die ganzzahlige Vielfache
voneinander sind. In diesen Fällen ergeben sich recht einfache
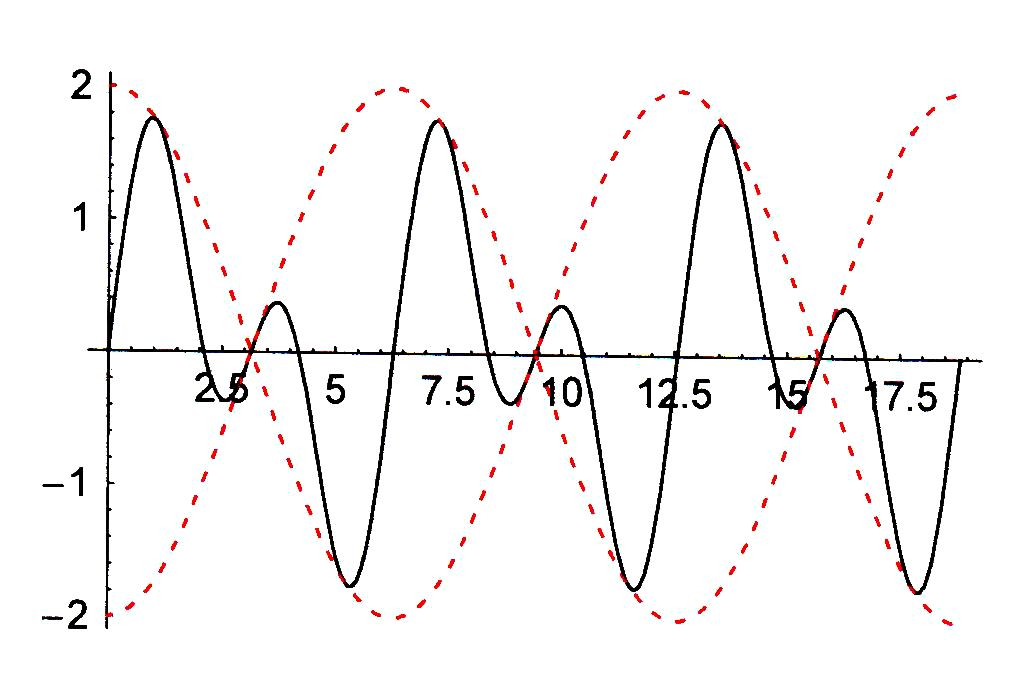
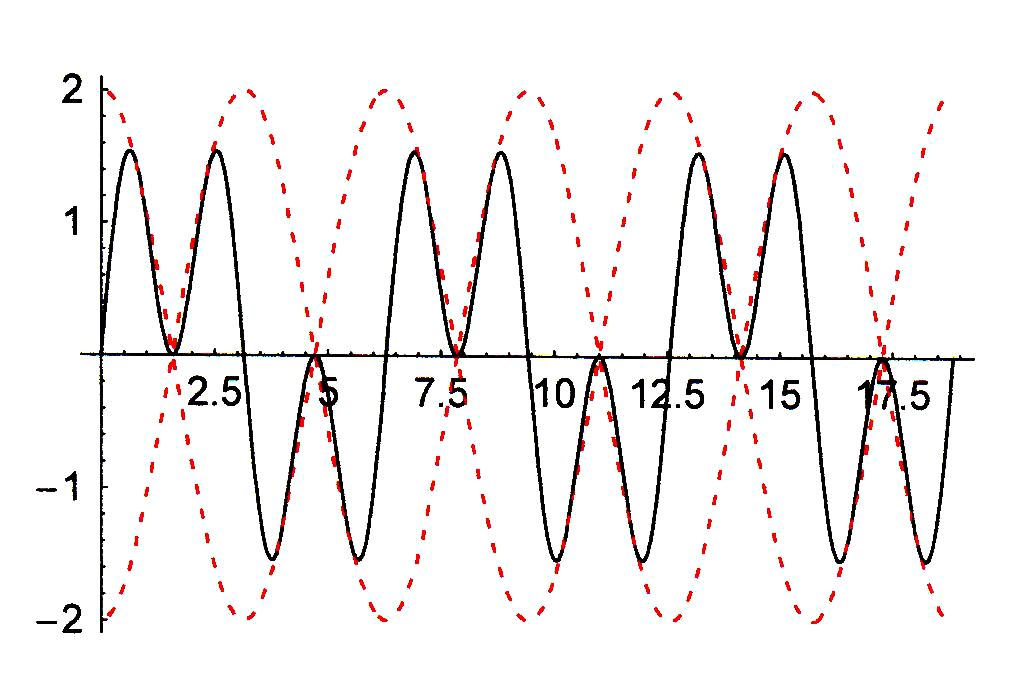
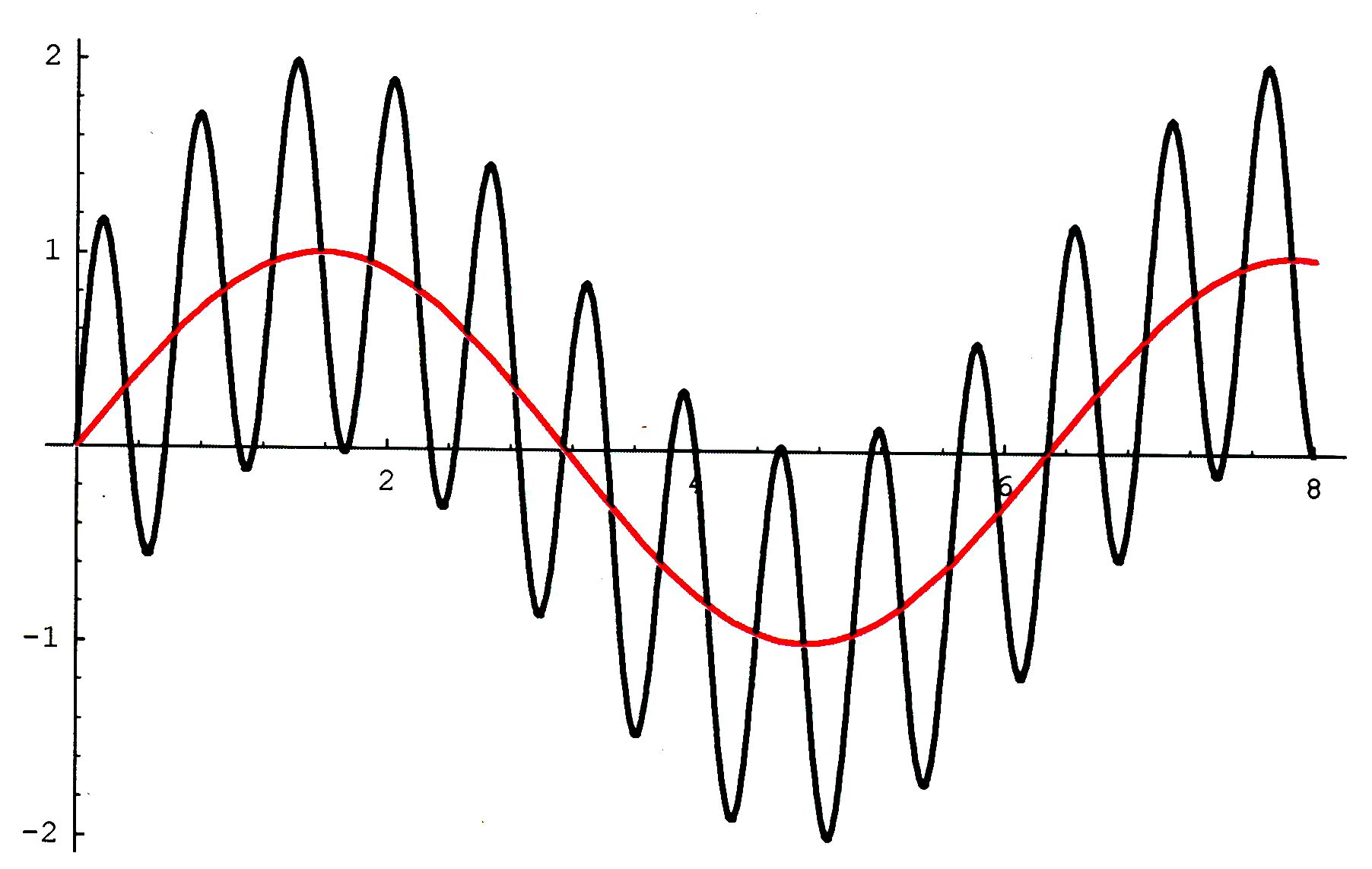
Überlagerungsmuster. In der Abbildung ist in Schwarz die
Überlagerung angegeben und in Rot der Graph, der die Größe der Amplitude
begrenzt. Man spricht von der Amplitudenmodulation. Man kann mit Hilfe von
Zeigerdiagrammen genauere Betrachtungen und Berechnungen zu den
Überlagerungen durchführen, die aber dem LK überlassen bleiben (Hinweis: noch in Arbeit).
Sonderfälle: - Überlagerung einer kleinen Frequenz mit
einer großen Frequenz In diesem Fall ist der Verlauf der Schwingung
der kleinen Frequenz (rot) noch gut in der Überlagerung (schwarz) erkennbar.
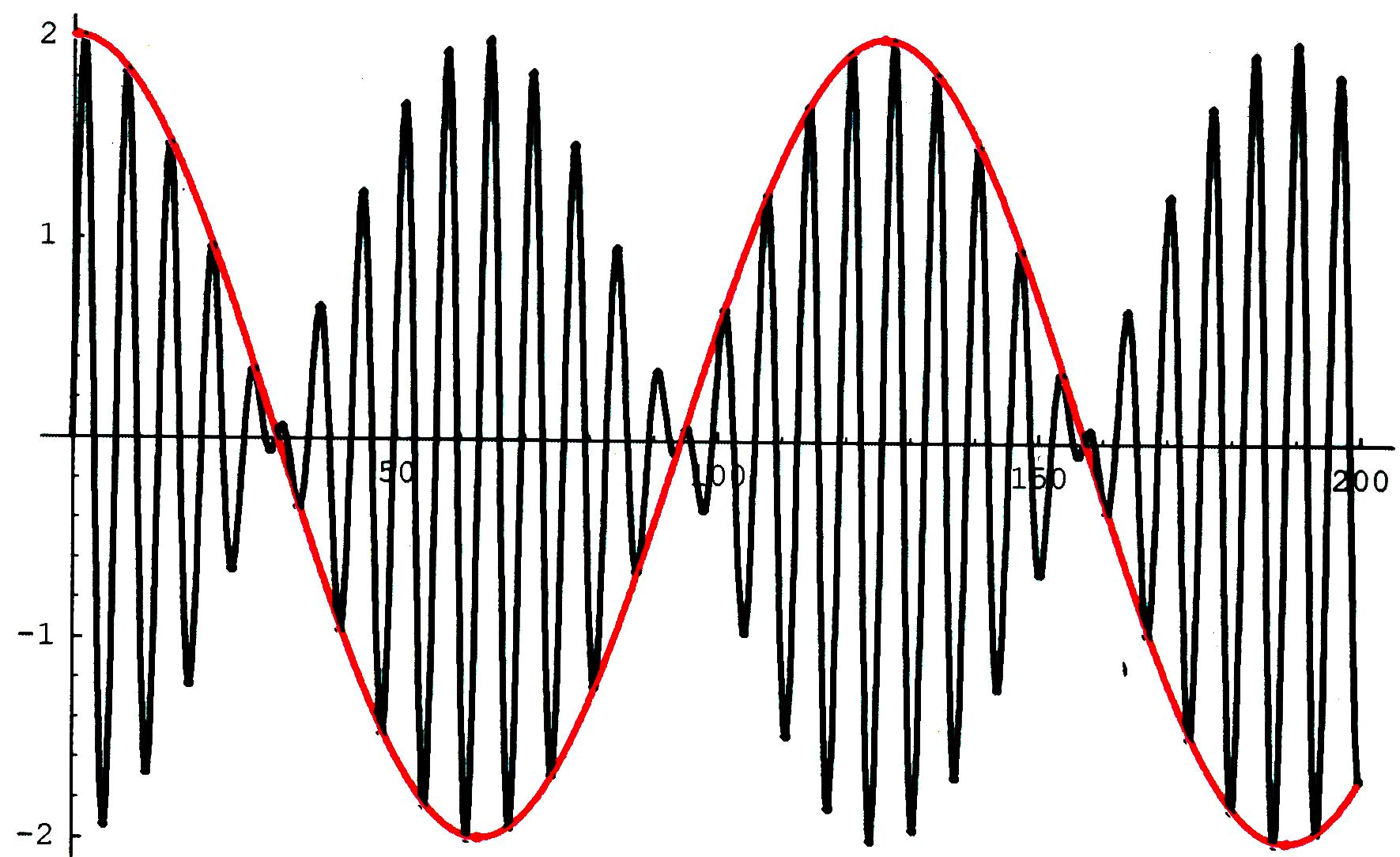
- Schwebungen: Überlagerung von Schwingungen
ähnlicher Frequenz Die Amplitudenmodulation erfolgt sehr langsam
(mit geringer Frequenz).
Wenn man zur Überlagerung Schallwellen
benutzt, kann man die Schwebung sehr schön anschaulich machen. Da die
Amplitude die Lautstärke widerspiegelt, wird bei einer Schwebung die
Lautstärke in regelmäßigen Abständen an- und abschwellen. Hierzu ein schönes Video:
|
|||||||||||||||||
|
|