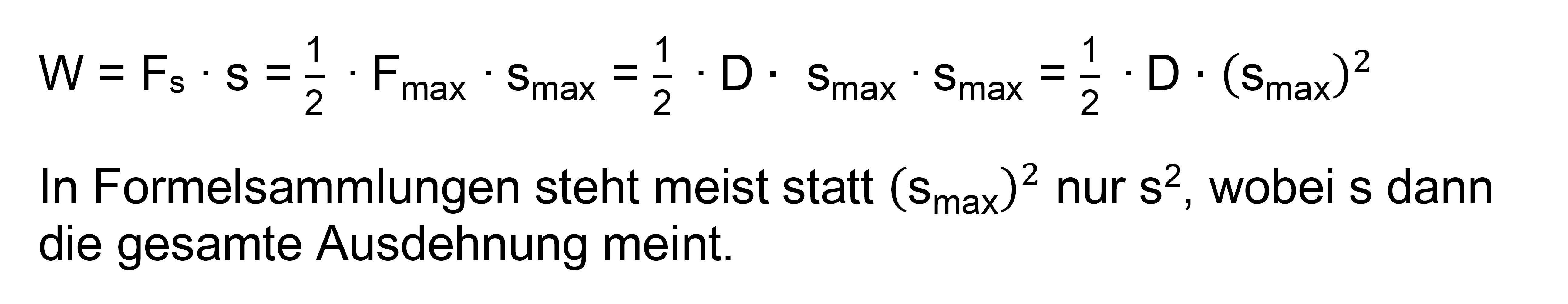|
Spannarbeit – Spannenergie Nach dem Hookeschen
Gesetz wollen wir uns jetzt mit der Spannarbeit bzw. Spann-energie
beschäftigen. Wenn man eine Feder
spannt, muss man ja gegen die Federkraft Arbeit verrichten. Man muss
Muskelkraft aufwenden, um die Feder zu spannen; oder eine Masse anhängen,
also Gewichtskraft ausüben, um für die Spannung der Feder zu sorgen. Die Formel zur
Berechnung der Arbeit lautete:
Wenn wir diese
Formeln hier benutzen wollen, bekommen wir ein Problem, da die
ausgeübte Kraft nicht konstant ist. Es gilt ja das
Hookesche Gesetz, also F = D * s, somit steigt die Muskelkraft proportional
zur Ausdehnung der Feder. Am Anfang muss man wenig Kraft ausüben, danach
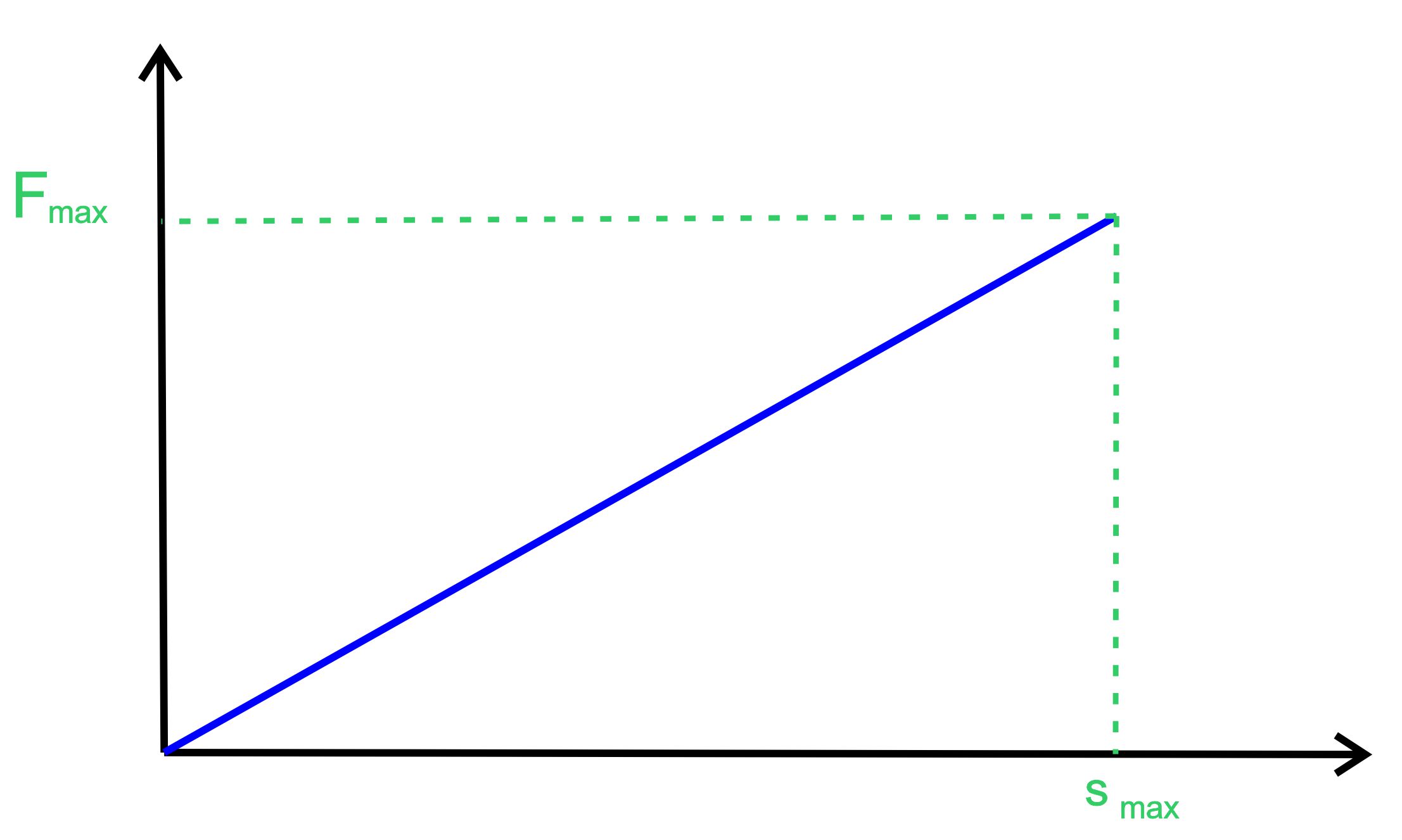
nimmt die Kraft kontinuierlich, eben proportional zu Ausdehnung, zu. In einer Abbildung
sieht das dann so aus:
Die Kraft steigt
linear mit der Ausdehnung an, also keine konstante Kraft. Wir können die
Formel nicht benutzen. Wir bedienen uns
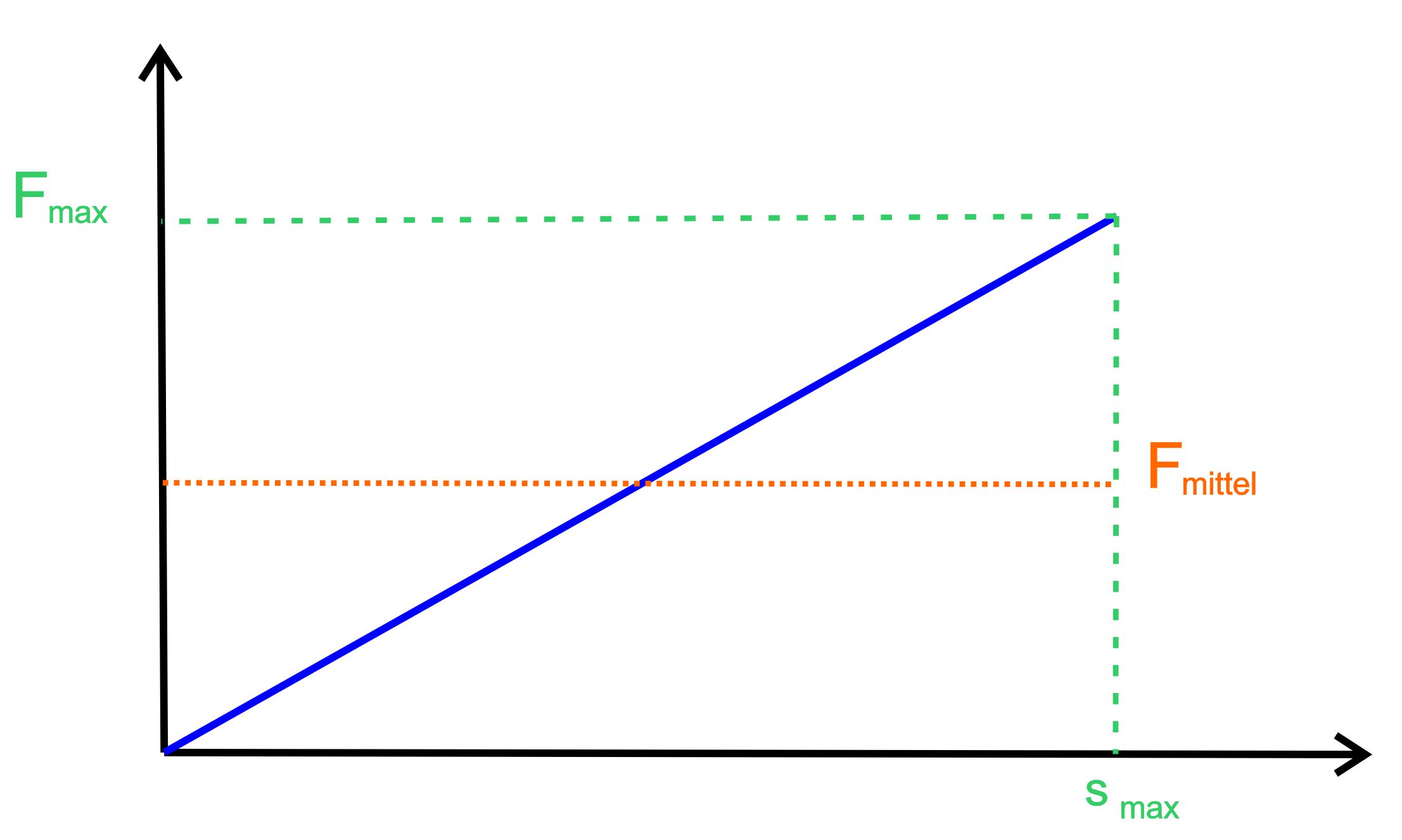
jetzt eines „Tricks“. Wenn wir am Anfang wenig Kraft aufwenden und am Schluss
viel Kraft, kann man sich doch eine „Durchschnittskraft“ bzw. „mittlere
Kraft“ vorstellen, die die gleichen Auswirkungen, also die gleiche Ausdehnung
wie die eigent- liche Kraft versucht. Diese Kraft dürfte
die Hälfte des Wertes der maximalen Kraft ausmachen. Ich habe die einmal in
die Abbildung eingetragen.
Man sieht diese
Durchschnittskraft ist zunächst größer als die eigentliche Kraft und am
Schluss kleiner als die eigentliche Kraft, so dass sie, auch aus
Symmetriegründen die gleiche Auswirkung haben dürfte. Mit dieser Kraft, da
sie ja als konstant angesehen wird, kann man die Arbeitsformel jetzt
benutzen. Es ergibt sich also:
Es ergibt sich somit
zusammenfassend für die Spannarbeit und damit für die in der gespannten Feder
gespeicherte Spannenergie:
Beispielaufgaben
|